Дан вписанный пятиугольник. Из вершины опустим три перпендикуляра на стороны пятиугольника, не выходящие из этой вершины. Основания перпендикуляров являются вершинами треугольника. Докажите, что площадь треугольника не зависит от выбора вершины пятиугольника.

На картинке площади красного и синего треугольников равны.

O и L — центр описанной окружности и точка Лемуана треугольника ABC. Докажите, что касательные к окружностям (AOL), (BOL) и (COL) в соответствующих вершинах треугольника пересекаются в одной точке.

G — точка пересечения медиан треугольника ABC. D — точка пересечения касательной к описанной окружности в точке A со стороной BC. Докажите, что красные углы равны.

красные углы не меняются

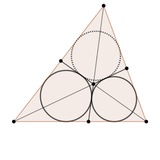
Треугольник с углами 40, 60 и 80 градусов.

Пожалуй самую красивую задачу, которую я придумал за последний год, вчера решали семиклассники на Московской устной олимпиаде. Само собой, что она была быть им по возрасту, то есть должна иметь решение без счета и тригонометрии. Предлагаю вам над ней тоже подумать. Обещаю: получите большое удовольствие!

Напомнилось тут в фейсбуке от Акопяна...

В США и Канаде trapezoid означает трапецию, а trapezium все остальные четырехугольники.

В остальном англоязычном мире: trapezium означает трапецию, а trapezoid все остальные четырехугольники.

Короче, английский очень сложный язык. Всегда надо помнить в журнал в какой стране вы отправляете свою математическую статью. И лучше бы в ней не было ни трапеций, ни четырехугольников.

Немного проспал(буквально) конец олимпиады, но вот моя задача с сегодняшней олимпиады. По-моему очень презабавно утверждение как факт...

Московская устная олимпиада по геометрии, 2025 год, 10-11 класс, Задача 6.

EGMO 2025, Problem 3

Пусть 𝐴𝐵𝐶 — остроугольный треугольник. Точки 𝐵, 𝐷, 𝐸 и 𝐶 лежат на одной прямой в указанном порядке, причём выполнено равенство 𝐵𝐷=𝐷𝐸=𝐸𝐶. Пусть 𝑀 и 𝑁 — середины отрезков 𝐴𝐷 и 𝐴𝐸 соответственно. Предположим, что треугольник 𝐴𝐷𝐸 является остроугольным, и пусть 𝐻 — его ортоцентр. На прямых 𝐵𝑀 и 𝐶𝑁 выбраны точки 𝑃 и 𝑄 соответственно таким образом, что точки 𝐷, 𝐻, 𝑀, 𝑃 лежат на одной окружности и попарно различны, а также точки 𝐸, 𝐻, 𝑁, 𝑄 лежат на одной окружности и попарно различны. Докажите, что точки 𝑃, 𝑄, 𝑁, 𝑀 лежат на одной окружности.

Задача от В.Н. Дубровского (извлечено из fb)

Доказать, что если BC и AD параллельны, то EC и AF тоже параллельны.

Вопрос от В.Н.:
This fact is the crucial point in a much more involved theorem, discussed in a number of papers, but I haven't seen it in such a concise form. Does anybody have a reference? Or an equally concise solution?

С удивлением вчера в очередной раз читал диспут про то, какие темы подходят, а какие не подходят для финала ВсОШ. Не слишком для меня удивительная особенность некоторых недавно выпустившихся и пока еще не выпустившихся:

до олимпиады недовольны тренировочными вариантами (в ваших тренировочных вариантах не те темы/не та сложность/задачи не того авторства — подчеркните нужное)

после олимпиады недовольны задачами олимпиады (в варианте олимпиады не те темы, что в были прошлые годы/не те темы, что проходят олимпиадники/не те темы, что проходят обычные школьники/слишком неразнообразное авторство/они бы еще ребус дали/они бы еще задачу на теорему Хана-Банаха дали — подчеркнуть нужное)

Кстати, про задачи на теорему Хана-Банаха. В 1998 году на финале ВсОШ была задача 11.8 авторства Алексея Яковлевича как раз на эту теорему.

Клетчатая фигура Ф обладает таким свойством: при любом заполнении клеток прямоугольника m×n числами, сумма которых положительна, фигуру Ф можно так расположить в прямоугольнике, чтобы сумма чисел в клетках прямоугольника, накрытых фигурой Ф, была положительна (фигуру Ф можно поворачивать). Докажите, что данный прямоугольник может быть покрыт фигурой Ф в несколько слоев.

Условия второго дня всеросса 2025