Всем привет! Еще одна классная новость, мимо которой я не могу пройти! Как раз про поступление на ту самую бакалаврскую программу от JetBrains. Можно не просто поступить, а получить еще и стипендию на обучение от JetBrains! Что для этого надо сделать? Подготовить документы, подать заявку до 12-го июня, пройти вступительный тест и, в случае успеха, пройти собеседование! А после этого учиться в очень классном месте у очень крутых преподавателей и купаться круглый год!
Admissions for Computer Science and Artificial Intelligence (CSAI) program are open until June 12! 💫
The CSAI BSc is a university program in Cyprus supported by JetBrains and is currently undergoing the accreditation process.
Don' miss out on your chance to get one of 15 JetBrains Scholarships. We expect to accept up to 40 students into the program.
Key Dates:
💸 Application deadline for the Scholarships: June 12 (11:59 pm UTC).
🧑💻 CSAI JetBrains Entrance Test: June 16, 2024
💼 Interviews for Top Performers: June 18–30, 2024
📅 Decisions will be made and sent out by July 1.
Have questions?
Сontact us via nup@jetbrains.com or Telegram and Whatsapp chats!
🚀Complete these four steps to be considered in the second wave:
1️⃣ Prepare the documents specified in this list.
2️⃣ Fill out the application form.
3️⃣ Send the documents and the application form to the application email address: student.advisor4@nup.ac.cy before June 12, 2024.
4️⃣ Prepare for the Entrance Test, and don’t miss the email with instructions. The Entrance Test will begin at 8:00 am UTC on June 16, 2024.
Learn more about the admission process here.
Good luck 🍀
Admissions for Computer Science and Artificial Intelligence (CSAI) program are open until June 12! 💫
The CSAI BSc is a university program in Cyprus supported by JetBrains and is currently undergoing the accreditation process.
Don' miss out on your chance to get one of 15 JetBrains Scholarships. We expect to accept up to 40 students into the program.
Key Dates:
💸 Application deadline for the Scholarships: June 12 (11:59 pm UTC).
🧑💻 CSAI JetBrains Entrance Test: June 16, 2024
💼 Interviews for Top Performers: June 18–30, 2024
📅 Decisions will be made and sent out by July 1.
Have questions?
Сontact us via nup@jetbrains.com or Telegram and Whatsapp chats!
🚀Complete these four steps to be considered in the second wave:
1️⃣ Prepare the documents specified in this list.
2️⃣ Fill out the application form.
3️⃣ Send the documents and the application form to the application email address: student.advisor4@nup.ac.cy before June 12, 2024.
4️⃣ Prepare for the Entrance Test, and don’t miss the email with instructions. The Entrance Test will begin at 8:00 am UTC on June 16, 2024.
Learn more about the admission process here.
Good luck 🍀
Задача с майских сборов. Группа некандидатов, день 1, задача 3, автор: Александр Терешин
В остроугольном треугольнике ABC, AB < AC, провели медиану AM и высоту BH. Касательные к окружности (ABC), проведенные в точках A и B, пересекаются в точке T. Окружность (BMT) повторно пересекает (ABC) в точке S. Докажите, что окружность (SAH) касается прямой AB.
В остроугольном треугольнике ABC, AB < AC, провели медиану AM и высоту BH. Касательные к окружности (ABC), проведенные в точках A и B, пересекаются в точке T. Окружность (BMT) повторно пересекает (ABC) в точке S. Докажите, что окружность (SAH) касается прямой AB.
Forwarded from Непрерывное математическое образование
https://zadachi.mccme.ru/2012/pics.html
сегодня вместо картинок по выходным — вот такая страница с разными геометрическими рисунками (на скриншоте несколько примеров) —
в честь 15 000 задач в ИПС «Задачи по геометрии»
и напомним отзывы коллег к предыдущему юбилею — https://old.mccme.ru/head/news/zadachi10000.htm
сегодня вместо картинок по выходным — вот такая страница с разными геометрическими рисунками (на скриншоте несколько примеров) —
в честь 15 000 задач в ИПС «Задачи по геометрии»
и напомним отзывы коллег к предыдущему юбилею — https://old.mccme.ru/head/news/zadachi10000.htm
Продолжаем субботнюю традицию! Еще одна классная точка, которая мне очень нравится и довольно часто возникает в задачах. Она тесно связана с предыдущими, что дает о ней много дополнительной информации!
Forwarded from Математические кружки | «МТ кружки»
Please open Telegram to view this post
VIEW IN TELEGRAM
В задаче 4, кстати, действительно очень крутая история ее создания и решения! А решение и аппарат для этого решения, насколько я знаю, придумал абсолютно легендарный геометр Виктор Абрамович Залгаллер.
Есть, кстати, несколько записанных диалогов с Залгаллером, если вы интересуетесь математикой и ее историей, это очень интересно.
https://youtu.be/1ZJBraHCpbA?si=66CrFaV_uWSA8rzh
Есть, кстати, несколько записанных диалогов с Залгаллером, если вы интересуетесь математикой и ее историей, это очень интересно.
https://youtu.be/1ZJBraHCpbA?si=66CrFaV_uWSA8rzh
YouTube
В.А. Залгаллер рассказывает 2
Запись сделана в Реховоте (Израиль) 30.10.2009
Всем привет! Немножечко спама вам в ленту! Опять неумолимо приближается лето и ваши любимые преподаватели уже чувствуют, что еще чуть-чуть и можно будет, наконец, вздохнуть с облегчением, никого не учить и отдохнуть. А что же делать вам? Как провести лето с пользой?
Как и год назад для вас есть куча разных лагерей, интенсивов, вебинаров, курсов и пр., на которых вы сможете отвлечь себя от ненавистного летнего отдыха. Одно расстраивает — перерывы между летними школами, которые просто нечем заполнить. Да и в летних школах с лагерями, порой, остается еще куча свободного времени, которое просто некуда засунуть. Ну действительно, не идти же гулять и дышать свежим воздухом...
Короче, как и год назад Давид Юрьевич Бродский организует свои супер-мега-пупер-классные курсы по геометрии. В этом году есть возможность учиться на трех уровнях сложности — можно подобрать себе наиболее комфортный.
Что полезно знать
► Продолжительность — 3 месяца, то есть можно заниматься все лето
► Раз в неделю выкладывается 1-2 лекции с теоретическим материалом
► Раз в неделю предлагается серия задач, которая проверяется преподавателями через таксу Дусю
► Раз в неделю онлайн разбор с Давидом Юрьевичем, где вы ему можете задать самые неожиданные вопросы
► На каждой неделе будут челлендж-задачки для тех, кто решил все основные
► Все материалы курса доступны до конца курса и даже немного дольше
► Для тех, кто все-таки отвлекается на всякие там лагеря и летние олимпиады, типа IMO, предусмотрен сдвиг дедлайнов и сроков доступа к материалам
Короче, заниматься можно в довольно лайтовом режиме и позволять себе паузы, и при этом круто прокачать себе геометрию всего за одно лето.
За подробностями ныряйте по ссылке
Ну и картинка к посту нужна. Вот вам одна из самых красивых задач Давида Юрьевича — задача через которую я вообще узнал о существовании такого человека.
Оказывается, ортоцентр треугольника с вершинами в серединах биссектрис лежит на прямой Эйлера исходного.
Как и год назад для вас есть куча разных лагерей, интенсивов, вебинаров, курсов и пр., на которых вы сможете отвлечь себя от ненавистного летнего отдыха. Одно расстраивает — перерывы между летними школами, которые просто нечем заполнить. Да и в летних школах с лагерями, порой, остается еще куча свободного времени, которое просто некуда засунуть. Ну действительно, не идти же гулять и дышать свежим воздухом...
Короче, как и год назад Давид Юрьевич Бродский организует свои супер-мега-пупер-классные курсы по геометрии. В этом году есть возможность учиться на трех уровнях сложности — можно подобрать себе наиболее комфортный.
Что полезно знать
► Продолжительность — 3 месяца, то есть можно заниматься все лето
► Раз в неделю выкладывается 1-2 лекции с теоретическим материалом
► Раз в неделю предлагается серия задач, которая проверяется преподавателями через таксу Дусю
► Раз в неделю онлайн разбор с Давидом Юрьевичем, где вы ему можете задать самые неожиданные вопросы
► На каждой неделе будут челлендж-задачки для тех, кто решил все основные
► Все материалы курса доступны до конца курса и даже немного дольше
► Для тех, кто все-таки отвлекается на всякие там лагеря и летние олимпиады, типа IMO, предусмотрен сдвиг дедлайнов и сроков доступа к материалам
Короче, заниматься можно в довольно лайтовом режиме и позволять себе паузы, и при этом круто прокачать себе геометрию всего за одно лето.
За подробностями ныряйте по ссылке
Ну и картинка к посту нужна. Вот вам одна из самых красивых задач Давида Юрьевича — задача через которую я вообще узнал о существовании такого человека.
Оказывается, ортоцентр треугольника с вершинами в серединах биссектрис лежит на прямой Эйлера исходного.
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
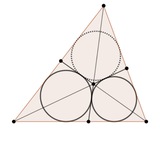
Пока самая красивая задача этого сезона. LMAO 2024 P3. Дан равносторонний оранжевый треугольник и точка P на его вписанной окружности. Точку P отразили относительно сторон оранжевого треугольника и получили красный треугольник. Далее отразили точку P относительно сторон красного треугольника и получили черный треугольник. Докажите, что описанная окружность черного треугольника касается вписанной и описанной оранжевого.
Задача от Василия Мокина! Предлагалась на зимних сборах в сезоне 2022/2023.
Даны две зеленые окружности одна внутри другой. Две красные окружности с красными центрами и две синие окружности с синими центрами касаются одной зеленой внутренним и одной зеленой внешним образом. Четырехугольник с вершинами в красных и синих центрах - трапеция. Тогда одна из диагоналей четырехугольника, образованного парами внешних касательных к красным и к синим окружностям перпендикулярна основанию этой трапеции.
Даны две зеленые окружности одна внутри другой. Две красные окружности с красными центрами и две синие окружности с синими центрами касаются одной зеленой внутренним и одной зеленой внешним образом. Четырехугольник с вершинами в красных и синих центрах - трапеция. Тогда одна из диагоналей четырехугольника, образованного парами внешних касательных к красным и к синим окружностям перпендикулярна основанию этой трапеции.