Квадрат ABCD, точка Е выбрана так, что АВ+ВЕ=АС

Доказать, что АЕ — биссектриса угла ВАС?

Теорема Дезарга = Теорема Паскаля.
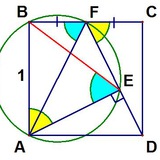
Хотим например доказать теорему Дезарга для выделенных цветных треугольников. Тогда по обратной теореме Паскаля получаем, что красные точки на одной конике. Применяя теорему Паскаля для них, но в другом порядке получаем нужную коллинеарность.

Кривизна окружности - это единица, деленная на ее радиус. Сумма кривизн окружностей в цепочке Штейнера остается неизменной при ее вращении, таким образом, является инвариантом. Кроме того, инвариантом является сумма k степеней кривизн, где k - любое натуральное число, меньшее числа окружностей в цепочке.

https://www.geogebra.org/classic/dqwpzzae

Подробности в статье:
https://arxiv.org/pdf/1811.08030

а) запишем для N-мерного куба количество вершин, количество всевозможных прямых через пары вершин, количество всевозможных плоскостей через тройки вершин… что за последовательность получится?

(например, для N=3 получается последовательность 8,28,20)

б) доказать, что эта последовательность всегда унимодальна (до какого-то момента возрастает, потом убывает)

(первый пункт — по мотивам вопроса Антона Авдеева в чате; ответа не знаю

второй пункт — по мотивам недавней филдсовской премии June Huh; унимодальность такой последовательности для произвольного набора точек — насколько понимаю, остается открытой проблемой уже больше 50 лет)

Высоты AA' и BB' треугольника ABC пересекаются в точке H. Точки X и Y – середины AB и CH. Доказать, что прямые XY и A'B' перпендикулярны.

// к дню рождения А.А.Заславского — пусть здесь будет такая его задача с ММО/Тургора-2005

Конспект Владимира Сергеевича Захарова к небольшому семинару по формуле Адамара для расчёта объёмов.

в новый Квант (№2 за 2025 год) вошла статья Ф.Бахарева и Г.Челнокова про Why-точки, полуописанные окружности и прямую Эйлера

https://biblio.mccme.ru/node/281875

ранее на эту тему: https://tttttt.me/olympgeom/1265

Проекциями некоторого треугольника на каждую из двух перпендикулярных плоскостей являются а) правильные; б) равнобедренные прямоугольные треугольники. Могут ли они быть неравными?

// А.Д.Блинков рассказал задачу

Приятная геометрия с сегодняшнего устного тура Турнира Городов.

На плоскости расположены круг и правильный 100-угольник, имеющие одинаковые площади. Какое наибольшее число вершин 100-угольника могут находиться внутри круга?

Любопытно дополнительно подумать, можно ли что-то разумное в трехмерном пространстве спросить по аналогии?

ABCD квадрат, O его центр, BE=BF. Доказать, что точки CKLON лежат на одной окружности.

// задача M2826 из Кванта, предложил А.Палеев (9 кл.)

Теорема Сильвестра-Галлаи утверждает, что для любого конечного числа точек на плоскости, не лежащих на одной прямой, существует прямая, проходящая ровно через две точки данного множества.

Разумно сформулировать аналогичный вопрос для пространства:

Верно ли, что для любого конечного числа точек в пространстве, не лежащих в одной плоскости, существует плоскость, проходящая ровно через три неколлинеарные точки данного множества?

Интересно, что ответ здесь отрицательный. Попробуйте придумать какие-то контр-примеры.