Forwarded from Ботаем геому
Условия прошедшей сегодня устной олимпиады по геометрии!
Если писали тур, расскажите, какие задачи вам понравились/не понравились.
Решения появятся в течении следующей недели
Если писали тур, расскажите, какие задачи вам понравились/не понравились.
Решения появятся в течении следующей недели
Стартует спецкурс от Ивана Кухарчука и Леонида Шатунова на платформе Дабромат, будет про продвинутую геометрию в треугольнике, подробнее можно прочитать по ссылке, должно быть интересно.
Стоимость курса: 14 900 рублей
Стоимость курса: 14 900 рублей
dabromat.ru
Программа спецкурс Кухарчука
Forwarded from Олимпиадная геометрия
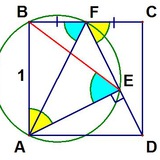
Слишком много дизлайков... Вот вам тогда задача с командной олимпиады проходящего сейчас Уральского турнира (63-го? я сбился со счета...)
CM — медиана равнобедренного остроугольного треугольника ABC (AB = BC). Точка D на отрезке CM такова, что AD — внешняя биссектриса угла MDB. Точка E на отрезке CM такова, что CE = BD. Докажите, что BE = AD.
CM — медиана равнобедренного остроугольного треугольника ABC (AB = BC). Точка D на отрезке CM такова, что AD — внешняя биссектриса угла MDB. Точка E на отрезке CM такова, что CE = BD. Докажите, что BE = AD.
Геометрия-канал
USEMO 2024 P3. Автор: Matsvei Zorka. Докажите равенство зеленых.
Давайте еще доп вопросик. Как построить точки P и Q?
Геометрия-канал
USEMO 2024 P3. Автор: Matsvei Zorka. Докажите равенство зеленых.
Для тех кому эта задача кажется сложной. Есть более простая задача и очень полезная!
Forwarded from Школа "Лес"
#онлайн_лекция
Друзья, 16 ноября в 18:00 по московскому времени состоится очередная онлайн-лекция нашего лектория!
На этот раз Полина Романова расскажет про то, как принципы геометрии используются в рисовании.
🔗 Трансляция произойдёт по этой ссылке.
⏰ Добавьте напоминание себе в календарь, чтобы не забыть.
Делитесь в комментариях своими любимыми скетчами с Инктобера, и до встречи в следующую субботу!
Друзья, 16 ноября в 18:00 по московскому времени состоится очередная онлайн-лекция нашего лектория!
На этот раз Полина Романова расскажет про то, как принципы геометрии используются в рисовании.
🔗 Трансляция произойдёт по этой ссылке.
⏰ Добавьте напоминание себе в календарь, чтобы не забыть.
Делитесь в комментариях своими любимыми скетчами с Инктобера, и до встречи в следующую субботу!
Forwarded from Фулл и точка
#красота_спасет_мир #разбор
Встречайте❗️Фантастический коллаб года 🔥
Специально для вас мы побывали в самом сердце белорусского олимпиадного математического движа 🧡— в гостях у крутейших авторов канала Geometry Belarus 😎
В этом выпуске ( тык - тык ) вас ждет авторский разбор одной из лучших (по версии Фулл и точка) геометрий года от легендарного призера международной математической олимпиады Матвея Зорько 🤩
Задача, которую мы будем разбирать, прогремела во всех геометрических пабликах, но для тех кто пропустил — условие и картинку мы оставляем в комментариях к посту 👇
Подумайте немного 🤔 прежде чем смотреть видео, чтобы получить настоящий кайф от неожиданного сюжетного поворота 😍
И как приятный бонус — в конце видео вас ждет конкурс с потрясающими белорусскими призами 🎁
Наливайте себе кружечку горячего чая ☕️, тыкайте на ссылочку 👉 тык - тык 👈
Прыемнага вам прагляду🎬
Встречайте❗️Фантастический коллаб года 🔥
Специально для вас мы побывали в самом сердце белорусского олимпиадного математического движа 🧡— в гостях у крутейших авторов канала Geometry Belarus 😎
В этом выпуске ( тык - тык ) вас ждет авторский разбор одной из лучших (по версии Фулл и точка) геометрий года от легендарного призера международной математической олимпиады Матвея Зорько 🤩
Задача, которую мы будем разбирать, прогремела во всех геометрических пабликах, но для тех кто пропустил — условие и картинку мы оставляем в комментариях к посту 👇
Подумайте немного 🤔 прежде чем смотреть видео, чтобы получить настоящий кайф от неожиданного сюжетного поворота 😍
И как приятный бонус — в конце видео вас ждет конкурс с потрясающими белорусскими призами 🎁
Наливайте себе кружечку горячего чая ☕️, тыкайте на ссылочку 👉 тык - тык 👈
Прыемнага вам прагляду
Please open Telegram to view this post
VIEW IN TELEGRAM
YouTube
Geometry Belarus | #maths #math #mathematics #geometry #математика #геометрия #belarus
Приехали в гости в Беларусь
Таймкоды:
0:09 Начало
1:16 Задача Матвея
2:11 Переформулировка задачи Матвея
9:50 Почему угол 45
12:42 Конкурс!
Таймкоды:
0:09 Начало
1:16 Задача Матвея
2:11 Переформулировка задачи Матвея
9:50 Почему угол 45
12:42 Конкурс!
Forwarded from NeuroGeometry (Петр Ким)
Задача 56:
Автор - Григорий Забазнов
Источник: MGO 2024, задача 4
На сторонах AB и AC треугольника ABC выбраны точки E и F соответственно так,что B,E,F,C лежат на одной окружности. Прямые BF и CE пересекаются в точке K. Отражение прямой AK относительно биссетрисы угла BAC пересекает BF и CE в точках M и N.
Доказать, что если окружность (MKN) касается BC, то она касается и EF.
Автор - Григорий Забазнов
Источник: MGO 2024, задача 4
На сторонах AB и AC треугольника ABC выбраны точки E и F соответственно так,что B,E,F,C лежат на одной окружности. Прямые BF и CE пересекаются в точке K. Отражение прямой AK относительно биссетрисы угла BAC пересекает BF и CE в точках M и N.
Доказать, что если окружность (MKN) касается BC, то она касается и EF.
Forwarded from Геометрия с Ниловым
Отношение длин касательных к эллипсу равно отношению радиусов вписанных окружностей (синих) и корню кубическому из отношения радиусов соприкасающихся окружностей (красных), касающихся эллипса в тех же точках. Второе утверждение - теорема Лиувилля.
Forwarded from Геометрия от Волчкевича
Верю — не верю!
Некоторые из предлагаемых шести утверждений на плоскости верны в общем случае. Отметьте их.
Некоторые из предлагаемых шести утверждений на плоскости верны в общем случае. Отметьте их.
Anonymous Poll
71%
1. У любого пятиугольника есть тупой угол.
37%
2. Шесть прямых могут иметь ровно 7 точек пересечения.
46%
3. Любую трапецию можно разрезать на две прямоугольные трапеции.
37%
4. Окружность, вписанная в треугольник со сторонами 4, 5 и 7, касается его средней линии.
46%
5. Сумма трех углов вписанного в окружность шестиугольника равна 360 градусов.
31%
6. Только правильный треугольник можно разрезать на три равных треугольника.
Forwarded from Геометрия с Ниловым
Пусть X и Y - проекции ортоцентра H треугольника ABC на внутреннюю и внешнюю биссектрисы угла B. Докажите, что прямая XY проходит через середину стороны AC.
Шедевр от Антона Тригуба. Источник.
https://youtu.be/fEinV81foBA
«…одна и та же задача может иметь “вложенные“ в нее интересные частные случаи, и в то же время может оказаться “вложенной” в более общую теорему. О примерах таких “математических матрёшек” рассказывает Павел Александрович Кожевников…»
здесь уже было это видео — но хочется повторить
доходит, кстати, как раз до кубических кривых
«…одна и та же задача может иметь “вложенные“ в нее интересные частные случаи, и в то же время может оказаться “вложенной” в более общую теорему. О примерах таких “математических матрёшек” рассказывает Павел Александрович Кожевников…»
здесь уже было это видео — но хочется повторить
доходит, кстати, как раз до кубических кривых
YouTube
Павел Кожевников | «Математические матрёшки»
Матрёшка - не только традиционный сувенир, но и повод взглянуть по-новому на некоторые математические сюжеты: одна и та же задача может иметь "вложенные" в нее интересные частные случаи, и в то же время может оказаться "вложенной" в более общую теорему. О…
Квадрат разрезан на прямоугольники. В каждом прямоугольнике отмечена одна сторона. Доказать, что сумма длин отмеченных сторон не меньше стороны квадрата.
Forwarded from Фулл и точка
11th-IGO_2024_English.pdf
1.1 MB