Геометрия-канал
Cevian nest theorem.
Вот картинка, которая сразу решает задачу. При этом объясняет почему эта теорема очень крутая...
❤16😱10🥱3👎1
если давно хотели изучить какое-нибудь доказательство теоремы Морли — то вот, например, свежий ролик: https://youtu.be/sfYUM20aAZA
YouTube
✓ Самое короткое доказательство теоремы Морли о трисектрисах | Ботай со мной #146 | Борис Трушин
Сегодня поговорим про одно короткое доказательство теоремы Морли о трисектриссах.
Теорема. Точки пересечения смежных трисектрис углов произвольного треугольника (то есть лучей, делящих угол на три равных угла) являются вершинами правильного треугольника.…
Теорема. Точки пересечения смежных трисектрис углов произвольного треугольника (то есть лучей, делящих угол на три равных угла) являются вершинами правильного треугольника.…
❤18👍4
Forwarded from Олимпиадная геометрия
Чешско-Австрийско-Польско-Словацкий матч 2024 (растут!)
В четырехугольнике ABCD
AB=BC=CD. На лучах CA и BD выбрали точки X и Y соответственно так, что BX=CY. Докажите, что середины BX, CY, DX, AY лежат на одной окружности.
В четырехугольнике ABCD
AB=BC=CD. На лучах CA и BD выбрали точки X и Y соответственно так, что BX=CY. Докажите, что середины BX, CY, DX, AY лежат на одной окружности.
❤15
Наверное уже была в этом канале, но как всегда можно придумать крутое доказательство, а не самое известное, которое конечно тоже крутое. Докажите, что фокус вписанной параболы в треугольник лежит на его описанной окружности
😱8❤6🔥2👍1
Forwarded from ppetya
Сегодня много узнал о Паппе -- если почти ничего не знать, то иногда можно много узнать.
Не знал его теорему о площадях. Темная площадь (двух произвольных параллелограммов на двух сторонах треугольника) равна серой (площадь третьего, темного параллелограмма, построенного по двум темным) площади -- серый параллелограмм строится по темным строится на рисунке.
Не знал его теорему о площадях. Темная площадь (двух произвольных параллелограммов на двух сторонах треугольника) равна серой (площадь третьего, темного параллелограмма, построенного по двум темным) площади -- серый параллелограмм строится по темным строится на рисунке.
❤13👍1
Forwarded from Geometry Ukraine (Mykhailo Sydorenko)
Простенька авторська.
Виявилося, що описане коло трикутника дотикається до описаного кола трикутника, сформованого стороною та двома серединними перпендикулярами до інших двох сторін. Доведіть що точка дотику цих кіл -- діаметрально протилежна до однієї з вершин.
Виявилося, що описане коло трикутника дотикається до описаного кола трикутника, сформованого стороною та двома серединними перпендикулярами до інших двох сторін. Доведіть що точка дотику цих кіл -- діаметрально протилежна до однієї з вершин.
👍16👎12😁3🥱3❤2🔥2🤔2
Ладно в шортлисте IMO есть прям хорошая задача...
🔥5
Forwarded from Записки юного геометра на пенсии (Щербатов Ярослав)
Тоже крепкий орешек по построению(ну или кто-то сроить не умеет).
IMO Shortlist 2023, G-3(https://www.geogebra.org/geometry/encgkzsy)
#IMOSL #IMOSL2023
IMO Shortlist 2023, G-3(https://www.geogebra.org/geometry/encgkzsy)
#IMOSL #IMOSL2023
❤8
Forwarded from Геометрия с Ниловым
Приятная задачка на теорему Пифагора. Чему равно расстояние до линии горизонта? Радиус Земли считать равным 6400 км, высоту глаз над уровнем моря 1,5 м. Покажите, что при увеличении высоты в x раз (например, если забраться на гору), расстояние до линии горизонта увеличивается примерно в корень из x раз.
❤20👍7🔥6
Forwarded from JustScience | Олимпиадная Математика (Константин Щербаков)
JustScience_листик_про_изогональное_сопряжение.pdf
41.5 KB
#Геометрия #Статья #Листик
Прикладываем статью Д.Прокопенко из Кванта про изогональное сопряжение — там можно найти доказательства полезных свойств изогонального сопряжения и примеры их использования
Здесь же прикреплена наша подборка задач, прорешав которую вы научитесь применять изогональное сопряжение в содержательных задачах!
Прикладываем статью Д.Прокопенко из Кванта про изогональное сопряжение — там можно найти доказательства полезных свойств изогонального сопряжения и примеры их использования
Здесь же прикреплена наша подборка задач, прорешав которую вы научитесь применять изогональное сопряжение в содержательных задачах!
❤18🔥5🤩4👍1
Forwarded from Я веду кружок (Konstantin Knop)
Метазадача на построение циркулем и линейкой
В прошлом месяце мы в Euclidea публиковали несколько задачек на построение "ржавым циркулем", то есть циркулем с фиксированным (единичным) радиусом (и, конечно, линейкой).
В следующем - хотим продолжить тему. В связи с этим у меня вопрос ко всем тем, кто любит решать задачки на построение: предложите нам самую интересную, на ваш вкус, задачу, которую надо было бы решить такими двумя инструментами.
Основные требования к задаче:
1) Минимум "материала" - чем проще исходный чертеж, тем лучше
2) Чтобы не работало традиционное построение
3) Чтобы в _достаточно коротком_ решении была какая-то интересная изюминка
Разумеется, если мы возьмем в конкурс вашу задачу, то укажем ее авторство.
Если хотите, можете предлагать задачи прямо в чатик. Если хотите в личку - @knop66
В прошлом месяце мы в Euclidea публиковали несколько задачек на построение "ржавым циркулем", то есть циркулем с фиксированным (единичным) радиусом (и, конечно, линейкой).
В следующем - хотим продолжить тему. В связи с этим у меня вопрос ко всем тем, кто любит решать задачки на построение: предложите нам самую интересную, на ваш вкус, задачу, которую надо было бы решить такими двумя инструментами.
Основные требования к задаче:
1) Минимум "материала" - чем проще исходный чертеж, тем лучше
2) Чтобы не работало традиционное построение
3) Чтобы в _достаточно коротком_ решении была какая-то интересная изюминка
Разумеется, если мы возьмем в конкурс вашу задачу, то укажем ее авторство.
Если хотите, можете предлагать задачи прямо в чатик. Если хотите в личку - @knop66
🔥4❤2👍1
Forwarded from Олимпиадная геометрия
Много геометрических каналов, конечно, развелось... проще перечислить тех, у кого их нет... но я попробую в почти случайном порядке перечислить те, что есть.
Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...
У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...
Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...
У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...
🔥15❤3
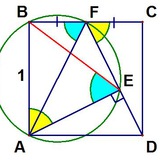
В четырехугольнике BCED три стороны равны (DB=BC=CE). Точка A внутри четырехугольника такова, что углы ABC и ACB равны \alpha и \beta, угол ABD равен 60°–(\alpha+2\beta)/3, а угол ACE равен 60°+(2\alpha+\beta)/3.
Докажите, что угол DAE равен \alpha+\beta
Источник: https://www.facebook.com/share/p/xn62fqozbsGxHcrt/?mibextid=oFDknk
Докажите, что угол DAE равен \alpha+\beta
Источник: https://www.facebook.com/share/p/xn62fqozbsGxHcrt/?mibextid=oFDknk
🔥8👍3❤1