задача, двойственная к предыдущей

(пусть будет и другая задача с визуально похожим условием, про которую в комментариях уже вспоминали)

доказать, что большой четырехугольник описанный

и чтобы завершить эту серию — утверждение, двойственное предыдущему, лемма о 6 окружностях

Просто задача.

KoMaL B. 5381

Кто-нибудь умеет просто доказывать такое утверждение: Дан треугольник ABC и точка P. Точки P_a,P_b,P_c симметричны относительно сторон ABC точке P. Точки O_a,O_b,O_c центры описанных окружностей треугольников PBC,PAC,PAB соответственно. Тогда, прямые AP_a,BP_b,CP_c пересекаются в одной точке тогда и только тогда, когда прямые AO_a,BO_b,CO_c пересекаются в одной точке

Статья на очень похожую задачу

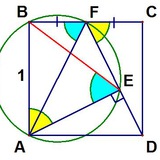
Зеленый четырехугольник — квадрат. Зеленый угол равен 45 градусов. Докажите, что разность красного и синего угла тоже 45 градусов.

Докажите, что точка пересечения высот треугольника, середины двух высот и основание третьей высоты лежат на одной окружности.

Может быть, кто-то в комментариях укажет первоисточник этой классической задачи

картинка на тему

«Что больше: 1⋅22+2⋅21+3⋅20+...+22⋅1 или 2²+4²+6²+...+22²?»

(из статьи А.Заславского в Квантике №6 за 2024 год)

Задача без картинки.
Дан треугольник ABC. Из точки A провели касательные к окружности с диаметром BC, которые касаются её в точках A_1,A_2. Аналогично определяются точки B_1,B_2,C_1,C_2. Докажите, что точки A_1,A_2,B_1,B_2,C_1,C_2 лежат на одной окружности.

Дан торт треугольной формы и коробка, которая имеет форму зеркально симметричного треугольника. Разрежьте торт на части и уложите их в коробку. Части можно поворачивать, но нельзя переворачивать

2024 RELMO 7. Можно ли восстановить(с помощью циркуля и линейки) разносторонний треугольник по точке Нагеля, точке Фейербаха и инцентру?

Дан прямоугольный треугольник ABC c углом A, равным 50 градусов. На катете BC взяли точки E и F так, что углы CAE и FAB равны по 10 градусов. Найти CE / FB

Назовём стулом [невыпуклый] шестиугольник с 5 прямыми углами.

а) Найти хотя бы один стул, который можно разбить на три стула, подобные исходному.
б*) Найти все такие стулья.

// К.Кноп предложил в mathpuz@fb

Задача В.В. Произволова.

Дан прямоугольный треугольник ABC с гипотенузой AB. На катетах AC и BC взяли такие точки X и Y, что AX = BC и BY = CX. Найдите угол между прямыми BX и AY.

А вот такое интересное "доказательство" теоремы Монжа (о трех колпаках), говорят принадлежит Акопяну

Заметим, что точка пересечения общих внешних касательных к двум окружностям обладает тем свойством, что любая прямая, проходящая через эту точку составляет равный угол с этими двумя окружностями. При этом верно и обратное утверждение. Следовательно, прямая, проходящая через два центра гомотетии, составляет равные углы со всеми тремя окружностями, а значит проходит и через третий центр гомотетии.

а вот еще одно доказательство теоремы Монжа: https://dev.mccme.ru/~merzon/pscache/monge.html

Предыдущие упоминания теоремы о колпаках в нашем канале:

https://tttttt.me/geometrykanal/2122

https://tttttt.me/geometrykanal/1982

https://tttttt.me/geometrykanal/105

Steinbart teorem. Предлагается не двигать и не считать в синусах.