В равнобедренном треугольнике вписанную окружность сдвинули на радиус параллельно основанию. Доказать, что теперь она касается описанной окружности.

upd: в комментариях также вариант для произвольного треугольника

Сегодня шикарная задачка (Автор: C. Августинович), которую я давал в этом году на кружке для 9 класса в школе Летово. Условие в две строчки, но для решения нужно озарение! Решение опубликуем в нашем Телеграм-канале позже, пусть у вас будет время подумать!

Верно ли, что из произвольного треугольника можно вырезать три равные фигуры, площадь каждой из которых больше четверти площади треугольника?

На закрытии LXXXVII Mосковской математической олимпиады обсуждали такую задачу В.В. Произволова

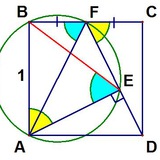
«На полосу положили квадрат, сторона которого равна ширине полосы, притом так, что его граница пересекла границу полосы в четырёх точках (см. рисунок). Докажите, что две прямые, проходящие накрест через эти точки, пересекаются на диагонали квадрата.»

Эту задачу, как и многие другие шедевры Вячеслава Викторовича, можно найти в книге «Задачи на вырост»:
https://www.mathedu.ru/text/proizvolov_zadachi_na_vyrost_2003/p0/

Я в свое время придумал на этом рисунке другую задачу, тоже симпатичную, и её взяли как weekly puzzle в Euclidea. Перевод: «Найдите сумму периметров двух треугольников».

Вот, кстати, похожая красивая задача про поиск угла. квадрат и равносторонний треугольник - найти угол на картинке

Сегодня рубрика “Геометрия для всех” и задача с базового Тургора 2022 года (Автор: М. Евдокимов). Как и во многих геометрических задачах нужно сначала понять, как устроена эта конструкция:

Пятиугольник ABCDE описан около окружности. Углы при его вершинах A, C и E равны 100⁰. Чему равен угол ACE?

Как использовать chat GPT для решения олимпиадных задач по геометрии и конструированию

Присоединяйтесь к зум конференции в пятницу 24 мая в 19:00 по Москве, где мы исследуем потенциал искусственного интеллекта в образовании, включая ChatGPT и другие передовые инструменты.

Что мы рассмотрим:
🚀 Новейшие инструменты искусственного интеллекта, такие как GPT-4, Google Gemini и Anthropic Claude 3.
🎓 Влияние ИИ на образование. Как ИИ меняет наш подход к обучению: от решения сложных задач по геометрии до улучшения навыков подготовки к экзаменам и программирования.
💫 Баланс ИИ и обучения: научитесь эффективно интегрировать ИИ, одновременно развивая критическое мышление и независимое обучение.

Лекцию проведет аспирант Киевского Политехнического Университета Даниил Теплов вместе с профессором Яковом Бен-Харавом, работавшим в области дифференциальной геометрии в Массачусетском Технологическом Институте.

Ссылка на зум:
https://us05web.zoom.us/j/9882232093?pwd=labFD4aUK3Xgxuf6ouaZq6ulcEPRVv.1&omn=84964387210

Идентификатор конференции: 988 223 2093
Код доступа: 12345
Запись будет.

https://zadachi.mccme.ru/2012/pics.html

сегодня вместо картинок по выходным — вот такая страница с разными геометрическими рисунками (на скриншоте несколько примеров) —

в честь 15 000 задач в ИПС «Задачи по геометрии»

и напомним отзывы коллег к предыдущему юбилею — https://old.mccme.ru/head/news/zadachi10000.htm

Две окружности касаются внутренним образом в точке T. Для каждой хорды XY, касающейся внутренней окружности, отметим середины дуг TX и TY. Доказать, что хорды, соединяющие эти середины, все проходят через одну точку.

(Квант M2773, Ф.Петров)

https://youtu.be/d6B7_YOPnY4

видеозапись лекции Дмитрия Швецова про биссектрисы (закрытие ММО, 19.05.2024)

В эллипс вписали две окружности. Окружность касается одной из них внешним, другой - внутренним образом. Тогда одна из ее общих хорд с эллипсом параллельна общей внутренней касательной к окружностям.

Одна из моих любимых задач. Про шестиугольник уж точно любимая.

Добрая задача. Докажите,что сумма площадей нечетных треугольников равна сумма площадей четных треугольников. (Одноцветные четырехугольники являются квадратами)

задача выше входит в серию утверждений, про которую можно узнать из статьи Ф.Нилова в Квантике №11 за 2020 год:
https://old.kvantik.com/art/files/pdf/2020-11.13-15.pdf

подвижные чертежи к статье:
https://kvantik.com/extra/parall/

Пока самая красивая задача этого сезона. LMAO 2024 P3. Дан равносторонний оранжевый треугольник и точка P на его вписанной окружности. Точку P отразили относительно сторон оранжевого треугольника и получили красный треугольник. Далее отразили точку P относительно сторон красного треугольника и получили черный треугольник. Докажите, что описанная окружность черного треугольника касается вписанной и описанной оранжевого.

Еще одна задача со всеросса, в которой помогает гипербола. Окружности omega и omega' симметричны относительно точки A. Всероссийская олимпиада 2022 9.8.(А.Шевцов)

Забавный факт.

Продолжаем с этой конструкцией.

доказать, что большой четырехугольник описанный