https://mccme.ru/nir/seminar/

в четверг (21.03) на семинаре учителей Наталия Стрелкова будет рассказывать про то как и зачем шевелить геометрию

19:00, столовая МЦНМО

На боковых сторонах треугольника откладывают от основания равные отрезки и строят на них как на диаметрах окружности. Доказать, что общие хорды всех таких пар окружностей проходят через одну точку.

// источник: https://tttttt.me/geometry_ukraine/549

Придумайте или найдите как можно больше "понятных прямых", которые касаются параболы с фокусом F и директрисой AM. Если хотите находить с геогеброй.

Теперь задача, которая сильно связана с предыдущей. (Всероссийская олимпиада школьников 2016 10.8.) Прямая, которая проходит через A,X,Y проходит через середину BC. Надо доказать, что окружности касаются.

На поверхности равногранного тетраэдра сидят два муравья. Докажите, что они могут встретиться, преодолев в сумме расстояние, не превосходящее диаметра окружности, описанной около грани тетраэдра.

Очередная задача от компьютера. Источник: 2022 Czech and Slovak Olympiad III. Закрашенный четырёхугольник является прямоугольником.

Очень крутая, но малоизвестная теорема (Теорема Витасса). Дан вписанный четырёхугольник ABCD. Его диагонали AC и BD пересекаются в точке P. Тогда, прямые Эйлера треугольников APB,BPC,CPD,APD пересекаются в одной точке. (Также можно задуматься, когда они являются параллельными)

Отличные плакаты Миши Панова!

https://zadachi.mccme.ru/plak/

Необычная для «Математических этюдов» премьера: «Теорема о двух кругах» https://etudes.ru/etudes/two-circles-theorem/ . Теорема даёт явное построение касательных к циклоидам – траекториям, описываемым фиксированной точкой окружности, катящейся без проскальзывания по некоторой гладкой линии.

Во-первых, необычная, так как просто объяснение геометрической теоремы. Но настолько красивой, что заслуживает своей отдельной экранизации. Кроме того, теорема дополняет цикл по понятию «огибающая» – сюжеты
«Парабола: изонить» https://etudes.ru/models/parabola-string-art/ ,
«Эллипс, гипербола, парабола: складывание листа бумаги» https://etudes.ru/models/conic-sections-paper-folding/ ,
«Кардиоида и нефроида» https://etudes.ru/models/cardioid-nephroid/ ,
«Каустики: нефроида и кардиоида» https://etudes.ru/etudes/caustic-nephroid-cardioid/ .

Теорема о двух круга, применённая к эпициклоидам, завершает доказательство того, что в цилиндрической чашке видна каустика в виде нефроиды, а в конической, когда лучи света параллельны образующей, – кардиоида.

Ну и во-вторых, премьера открывает новый жанр на Этюдах – повествование с анимированными рисунками.

Добрая задача про трапецию

Давно у нас не было геометрии. И сегодня новая 40-градусная задачка из серии "Геометрия для всех"!

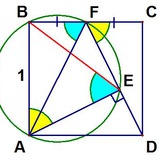
Вершины ломаной ABCD лежат на сторонах прямоугольника (см. рисунок). Все звенья ломаной равны, а два отмеченных на рисунке угла равны 40⁰. Чему равен угол CAD?

Пример, когда n=4 (прямые - это окружности, проходящие через бесконечно удаленную точку)

Пример, когда n=5 (прямые - это окружности, проходящие через бесконечно удаленную точку)

Добрая задача про равные окружности: красные окружности равны, докажите, что угол прямой

https://miro.com/app/board/uXjVKY1HfmI=/ & https://geometry.ru/dv.html — материалы по геометрии с сегодняшнего семинара учителей

Опять задача про Шалтая и Болтая. Закрашенный четырёхугольник является параллелограммом.

Даны две пересекающиеся окружности. Доказать, что длина отрезка BC не зависит от выбора точки A.

а кому это слишком просто — решите задачу Д.В.Прокопенко с устной олимпиады по геометрии 2010 года:

Серединные перпендикуляры к сторонам ВС и АС остроугольного треугольника АВС пересекают прямые АС и ВС в точках М и N. Пусть точка С движется по описанной окружности треугольника ABC, оставаясь в одной полуплоскости относительно АB (при этом точки A и B неподвижны). Докажите, что прямая MN касается фиксированной окружности.

можно считать, что всё это в качестве рекламы упомянутого семинара — вот, кстати, видеозапись: https://youtu.be/j-Z3-IfS8b4

Касательную к вписанной окружности треугольника отразили относительно биссекстрис его внешних углов. Докажите, что три полученные прямые ограничивают треугольник, равный исходному.