Forwarded from Непрерывное математическое образование
Дана окружность и точка A внутри нее. Как выглядит множество вершин C всевозможных прямоугольников ABCD, у которых вершины B и D лежат на нашей окружности?
(Такая задача с Московской математической олимпиады. Предлагается не только решить ее, но и понять, как она связана с другой задачей, которая здесь недавно была.)
(Такая задача с Московской математической олимпиады. Предлагается не только решить ее, но и понять, как она связана с другой задачей, которая здесь недавно была.)
Forwarded from Для учителей математики (Alexey Sgibnev)
Доклад Д.В. Прокопенко 8.12.22.
Доказательство некоторых классических формул. Дополнительные построения
Часть 1. Сама формула подсказывает как догадаться до дополнительных построений.
Часть 2. Дополнительные построения, связанные с треугольниками, трапециями, четырехугольниками и др. (достроить до треугольника, разрезание на трапеции, свертывание, отрезали и переложили...), а также превращения точек и прямых (например, центр вписанной окружности становится центром описанной окружности и т.д.
https://youtu.be/Vtoze6-tcXY
Доказательство некоторых классических формул. Дополнительные построения
Часть 1. Сама формула подсказывает как догадаться до дополнительных построений.
Часть 2. Дополнительные построения, связанные с треугольниками, трапециями, четырехугольниками и др. (достроить до треугольника, разрезание на трапеции, свертывание, отрезали и переложили...), а также превращения точек и прямых (например, центр вписанной окружности становится центром описанной окружности и т.д.
https://youtu.be/Vtoze6-tcXY
YouTube
Д.В.Прокопенко
Forwarded from Непрерывное математическое образование
https://anton-petrunin.github.io/puzzles/
https://arxiv.org/abs/0906.0290
для долгих зимних вечеров — книга PIGTIKAL («puzzles in geometry that I know and love») А.Петрунина
«This collection is about ideas, and it is not about theory. An idea might feel more comfortable in a suitable theory, but it has its own life and history, and it can speak for itself.
I am collecting these problems for fun, but they might be used to improve the problem-solving skills in geometry. Every problem has a short elegant solution — this gives a hint which was not available when the problem was discovered.»
https://arxiv.org/abs/0906.0290
для долгих зимних вечеров — книга PIGTIKAL («puzzles in geometry that I know and love») А.Петрунина
«This collection is about ideas, and it is not about theory. An idea might feel more comfortable in a suitable theory, but it has its own life and history, and it can speak for itself.
I am collecting these problems for fun, but they might be used to improve the problem-solving skills in geometry. Every problem has a short elegant solution — this gives a hint which was not available when the problem was discovered.»
Forwarded from Я веду кружок (Grigory Merzon)
Кухарчук-геометрия.pdf
54.5 KB
Иван Кухарчук пишет в вк:
«Олимпиадная геометрия в последнее время обогатилась кучей красивых техник, которые порой позволяют пробивать даже самые трудные гробы «за дешево». Однако, кажется, все эти приемы сложно выучить, а о некоторых из них многие вообще не знают.
В этом году я в экспериментальном формате на базе школы ЦПМ прочитал курс, охватывающий большинство известных мне самых современных олимпиадно-геометрических техник. Все материалы этого курса собраны в <pdf-файле> (там есть ссылки на видео занятий, презентации и листочки с задачами).»
«Олимпиадная геометрия в последнее время обогатилась кучей красивых техник, которые порой позволяют пробивать даже самые трудные гробы «за дешево». Однако, кажется, все эти приемы сложно выучить, а о некоторых из них многие вообще не знают.
В этом году я в экспериментальном формате на базе школы ЦПМ прочитал курс, охватывающий большинство известных мне самых современных олимпиадно-геометрических техник. Все материалы этого курса собраны в <pdf-файле> (там есть ссылки на видео занятий, презентации и листочки с задачами).»
Forwarded from Олимпиадная геометрия
Юрий Казаков (YuKa) задает интересный вопрос про вписанно-описанный пятиугольник
https://youtu.be/BklpHWNi0ig
https://youtu.be/BklpHWNi0ig
YouTube
Sum 1/r_i =const. Poncelet pentagon. Five mixtilinear in circles.
#Poncelet #bicentricpentagon #mixtilinearcircles
Сумма обратных радиусов mixtilinear окружностей для пятиугольника Понселе - инвариант (не зависит от положения пятиугольника). Кроме свойства для внутренних окружностей точно такое же свойство выполняется…
Сумма обратных радиусов mixtilinear окружностей для пятиугольника Понселе - инвариант (не зависит от положения пятиугольника). Кроме свойства для внутренних окружностей точно такое же свойство выполняется…
Forwarded from Непрерывное математическое образование
Квадрат разбит на N подобных прямоугольников. Каким может быть отношение сторон прямоугольника?
На рисунке все возможные варианты для N=3.
Больше картинок и разговоров:
1) https://johncarlosbaez.wordpress.com/2022/12/22/dividing-a-square-into-similar-rectangles/
2) https://johncarlosbaez.wordpress.com/2022/12/28/guillotine-partitions-and-the-hipparchus-operad/
На рисунке все возможные варианты для N=3.
Больше картинок и разговоров:
1) https://johncarlosbaez.wordpress.com/2022/12/22/dividing-a-square-into-similar-rectangles/
2) https://johncarlosbaez.wordpress.com/2022/12/28/guillotine-partitions-and-the-hipparchus-operad/
Геометрия-канал
Из центра каждой из двух данных окружностей проведены касательные к другой окружности. Доказать, что хорды, соединяющие точки пересечения касательных с окружностями (см. рис.), равны. (Такая ”теорема о глазных яблоках“. Если не пробовали — докажите, это не…
YouTube
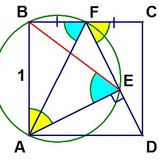
Докажите, что это прямоугольник
Решаем геометрическую задачу, пользуясь свойствами подобных треугольников.
У треугольника бывает не только вписанная окружность, но и полувписанные: касающиеся двух сторон и описанной окружности.
Как такую окружность построить (например, чтобы нарисовать в геогебре)? Помогает такое утверждение (и само по себе симпатичное): точки касания полувписанной окружности со сторонами и центр вписанной окружности лежат на одной прямой.
Предлагается это доказать.
Как такую окружность построить (например, чтобы нарисовать в геогебре)? Помогает такое утверждение (и само по себе симпатичное): точки касания полувписанной окружности со сторонами и центр вписанной окружности лежат на одной прямой.
Предлагается это доказать.
Тут народ пообсуждал некоторую вспомогательную окружность, связанную с треугольником, а я традиционно задумался над ее неинверсионным построением. И вот, придумалась задачка.
Дан треугольник ABC. Пусть K - точка касания вписанной окр. с AB, I_c - центр вневписанной окр., а D - точка пересечения прямой KI_c с серединным перпендикуляром к AB. Докажите, что окружность, описанная около ABD, касается вписанной окружности.
Дан треугольник ABC. Пусть K - точка касания вписанной окр. с AB, I_c - центр вневписанной окр., а D - точка пересечения прямой KI_c с серединным перпендикуляром к AB. Докажите, что окружность, описанная около ABD, касается вписанной окружности.
опубликованы задачи IX Иранской геометрической олимпиады, проходившей осенью: https://igo-official.com/wp-content/uploads/2023/01/IGO-2022_All-Exams.pdf
iran2022.pdf
168.7 KB
то же на русском и казахском языках
Forwarded from Непрерывное математическое образование
https://old.kvantik.com/art/files/pdf/2021-01.14-15.pdf
https://old.kvantik.com/art/files/pdf/2021-03.22-24.pdf
https://old.kvantik.com/art/files/pdf/2021-05.21-24.pdf
серия про сгибания бумаги в журнале «Квантик» (И.Сиротовский, А.Шкловер)
https://old.kvantik.com/art/files/pdf/2021-03.22-24.pdf
https://old.kvantik.com/art/files/pdf/2021-05.21-24.pdf
серия про сгибания бумаги в журнале «Квантик» (И.Сиротовский, А.Шкловер)
Хорошее простое упражнение на среднюю линию подарила нам диагностика «Математической вертикали».
Утверждение: Если в треугольнике медиана перпендикулярна средней линии, то он равнобедренный.
Постройте контрпример.
Утверждение: Если в треугольнике медиана перпендикулярна средней линии, то он равнобедренный.
Постройте контрпример.
Forwarded from Олимпиадная геометрия
Всем привет!
Посчастливилось поучаствовать в коллабе с Михаилом Громовым (канал Поступашки), Владиславом Вулем и Игорем Уколовым (канал Профиматика) и Wild Mathing. Получилось довольно интересное видео, в котором даются разные доказательства замечательного свойства трапеции. Наслаждайтесь)
https://youtu.be/8zBvcAWmHEI
Посчастливилось поучаствовать в коллабе с Михаилом Громовым (канал Поступашки), Владиславом Вулем и Игорем Уколовым (канал Профиматика) и Wild Mathing. Получилось довольно интересное видео, в котором даются разные доказательства замечательного свойства трапеции. Наслаждайтесь)
https://youtu.be/8zBvcAWmHEI
YouTube
Коллаб 4 каналов. 4 замечательные точки трапеции
Олимпиадная геометрия
YouTube - https://youtube.com/@OlympiadGeometry
VK - https://vk.com/olympgeom
Telegram - https://tttttt.me/olympgeom
Поступашки
YouTube - https://www.youtube.com/c/Postupashki
VK - https://vk.com/postypashki
Telegram - https://tttttt.me/postupashki…
YouTube - https://youtube.com/@OlympiadGeometry
VK - https://vk.com/olympgeom
Telegram - https://tttttt.me/olympgeom
Поступашки
YouTube - https://www.youtube.com/c/Postupashki
VK - https://vk.com/postypashki
Telegram - https://tttttt.me/postupashki…
#постоплачен
Иногда аналитику или специалисту по DS нужно подтянуть что-то по математике, чтобы решать более сложные задачи на работе. На курсе Яндекс Практикума можно раз и навсегда разобраться с тервером, линалом, матаном и статистикой. А потом — расти в карьере.
Учёбу удобно совмещать с работой: теория и практика будут в интерактивном тренажёре, который можно скачать на смартфон. А опытные преподаватели математики всегда на связи в чате, чтобы объяснить непонятное.
За 4 месяца обучения вы:
→ решите более тысячи задач в онлайн-тренажёре,
→ создадите 4 проекта для своего портфолио,
→ подготовитесь к собеседованиям с помощью симулятора.
Оцените формат и пройдите бесплатный вводный урок: https://practicum.yandex.ru/math-for-da-ds/
Иногда аналитику или специалисту по DS нужно подтянуть что-то по математике, чтобы решать более сложные задачи на работе. На курсе Яндекс Практикума можно раз и навсегда разобраться с тервером, линалом, матаном и статистикой. А потом — расти в карьере.
Учёбу удобно совмещать с работой: теория и практика будут в интерактивном тренажёре, который можно скачать на смартфон. А опытные преподаватели математики всегда на связи в чате, чтобы объяснить непонятное.
За 4 месяца обучения вы:
→ решите более тысячи задач в онлайн-тренажёре,
→ создадите 4 проекта для своего портфолио,
→ подготовитесь к собеседованиям с помощью симулятора.
Оцените формат и пройдите бесплатный вводный урок: https://practicum.yandex.ru/math-for-da-ds/
Forwarded from Непрерывное математическое образование
Ptolemyv3.pdf
641.7 KB
Anna Felikson. Ptolemy Relation and Friends
внутри не только теорема Птолемея, но и соотношения Плюккера, числовые фризы, кластерные алгебры… — вот это всё. и с цветными картинками
(https://amathr.org/ via П.Пушкарь)
внутри не только теорема Птолемея, но и соотношения Плюккера, числовые фризы, кластерные алгебры… — вот это всё. и с цветными картинками
(https://amathr.org/ via П.Пушкарь)
Неравнобедренный остроугольный треугольник ABC, AH — высота, AM — медиана, O — центр описанной окружности, отрезки AM и OH пересекаются в точке D, E— пересечение AB и CD, F — пересечение AC и BD.
Лучи EH и FH (красные) пересекают описанную окружность в точках X и Y. Доказать, что прямые CX, BY и AH пересекаются в одной точке.
(прислали задачу с регионального этапа ВсОШ сегодня)
Лучи EH и FH (красные) пересекают описанную окружность в точках X и Y. Доказать, что прямые CX, BY и AH пересекаются в одной точке.
(прислали задачу с регионального этапа ВсОШ сегодня)
Разработчик. Профпроба.
#реклама
Работать в IT перспективно и престижно. Особенно, если речь идет о профессии разработчика 😎
Но часто ребят (да и их родителей) терзают сомнения:
— Получится ли?
— А точно я этого хочу?
— А чем вообще занимается разработчик?
Мы верим: только практика помогает по-настоящему понять профессию и сделать осознанный выбор. Поэтому приглашаем старшеклассников на 4 часа погрузиться в реальные задачи разработчиков современной IT-компании.
На профпробе ребята познакомятся со всеми этапами разработки — от постановки задачи и создания дизайна до написания кода. Будет и бэкенд, и фронтенд🙌
Под руководством опытных разработчиков школьники откроют мир настоящего крутого IT:
▪️поработают с базой данных IT-системы, которая используется в крупных банках;
▪️создадут простейший код для автоматизации;
▪️напишут SQL-запросы для создания и выбора записей по условиям;
▪️напишут код веб-интерфейса страницы web-приложения.
12 марта (вскр), 12:00—16:00
Купить билет
По промокоду ГЕОМЕТРИЯ скидка 10%.
P. S. Знание каких-либо программ или языков программирования не требуется, всему научим 😎
Расписание других мероприятий можно посмотреть тут.
@profprobe
#реклама
Работать в IT перспективно и престижно. Особенно, если речь идет о профессии разработчика 😎
Но часто ребят (да и их родителей) терзают сомнения:
— Получится ли?
— А точно я этого хочу?
— А чем вообще занимается разработчик?
Мы верим: только практика помогает по-настоящему понять профессию и сделать осознанный выбор. Поэтому приглашаем старшеклассников на 4 часа погрузиться в реальные задачи разработчиков современной IT-компании.
На профпробе ребята познакомятся со всеми этапами разработки — от постановки задачи и создания дизайна до написания кода. Будет и бэкенд, и фронтенд🙌
Под руководством опытных разработчиков школьники откроют мир настоящего крутого IT:
▪️поработают с базой данных IT-системы, которая используется в крупных банках;
▪️создадут простейший код для автоматизации;
▪️напишут SQL-запросы для создания и выбора записей по условиям;
▪️напишут код веб-интерфейса страницы web-приложения.
12 марта (вскр), 12:00—16:00
Купить билет
По промокоду ГЕОМЕТРИЯ скидка 10%.
P. S. Знание каких-либо программ или языков программирования не требуется, всему научим 😎
Расписание других мероприятий можно посмотреть тут.
@profprobe
career.hflabs.ru
Мастер-класс в IT-компании для школьников
Мы расскажем об IT-специальностях и дадим примерить их на себя. Покажем, как в IT развиваются и технари, и гуманитарии. А еще подскажем, где и чему учиться, чтобы получить интересную профессию хорошо зарабатывать.