1) Существует ли тетраэдр, основания высот которого не принадлежат граням?
2) Существует ли выпуклый многогранник и точка внутри такая, что основания всех перпендикуляров, опущенных из нее на грани, не принадлежат граням?

Квадартура Луночки

По просьбам тех, кто был на пятничном рассказе Валентины Алексеевны на матклубе в Циферблате, выкладываем слайды.

Тем, кто не был, можно прочитать серию из двух статей в Квантике (начало и окончание) или публикацию на сайте Мел. Они очень хорошо написаны.

А еще на лекции была задача с картинки, можно попробовать с ней разобраться для разминки

1) Дан параллелограмм ABCD. Точки E и F выбраны на сторонах AD и AB так, что BE = DF. Отрезки BE и CF пересекаются в точке G. Докажите, что C лежит на биссектрисе угла BGD.

2) Докажите теорему Штейнера — Лемуса (если в треугольнике равны 2 биссектрисы, то этот треугольник является равнобедренным)

На плоскости даны семейство красных и семейство синих прямых. Известно, что в каждом семействе нет параллельных прямых. Зафиксируем некоторый угол. Для каждой синей прямой выберем (в случае, если это возможно) красную прямую, пересекающую ее под данным ориентированным углом, и отметим точку пересечения. Оказалось, что для любого угла все точки пересечения красных и синих прямых (пересекающимися под данным углом) лежат на одной окружности. Как могут быть устроены семейства красных и синих прямых? Например, это могут быть два пучка прямых. Я знаю еще только два примера.

Добрая задача.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.

Добрый день. Во вторник, 29 апреля в 15:30-16:30 по Москве, будет математический кружок 🟢

Title: Самозаклинивающиеся структуры

Speaker: Ф. K. Нилов

Аннотация:

Известно, что если на плоскости имеется конечный набор выпуклых фигур, внутренности которых не пересекаются, то среди этих фигур имеется хотя бы одна крайняя - такая, которую можно непрерывно передвинуть “на бесконечность” (за пределы большого круга, содержащего остальные фигуры), оставляя все остальные фигуры неподвижными и не пересекая их внутренности в процессе движения.

А что происходит в пространстве? На первый взгляд кажется, что должны быть справедливы аналогичные утверждения. Например, их можно доказать в частном случае, когда все тела являются шарами (для произвольной размерности). Однако в общем случае оказывается, что в пространстве имеет место феномен самозаклинивающихся структур. Самозаклинивающаяся структура — такой (конечный или бесконечный) набор выпуклых тел с непересекающимися внутренностями, что если зафиксировать все, кроме любого одного, оставшееся нельзя “унести на бесконечность”, не пересекая внутренности других тел в процессе движения.

Мы обсудим уже известные и новые стуктуры, построенные совсем недавно.


Zoom meeting link:
Zoom - Meeting ID: 853 1771 8785 Passcode: 549695
Link: https://us02web.zoom.us/j/85317718785?pwd=XS0bILZaREyt00pA2EJlu1zxaEHbDN.1

Приходите!

Номер 3 за 2025 год в продаже:
https://biblio.mccme.ru/node/286493

в Квант №3 вошла статья «Угол между радиусом и стороной» Ю.Блинкова и Д.Швецова

Тут есть очень короткое, но очень красивое решение

Дан треугольник ABC и окружность ω, которая касается сторон AB и AC и описанной окружности треугольника в точке D. Оказалось, что AD ⊥ BC. Докажите, что BD + CD = 2R, где R — радиус (ABC).

В правильном тетраэдре с ребром 1 через вершину проведено треугольное сечение. Доказать, что его периметр больше 2.

// Д.Мухин на семинаре учителей напомнил про такую задачу с московской окружной олимпиады-2011

https://classics.nsu.ru/schole/assets/files/18-1-schetnikov.pdf

в качестве картинок по выходным — статья А.И.Щетникова «Исламские геометрические орнаменты»

По-моему очень крутая задача про изогональное сопряжение с ЮМТ.
Дан треугольник ABC с парой изогонально сопряженных точек P и Q. На прямых CP, CQ, BP, BQ выбраны точки X, Y, Z, T соответственно так, что XY // ZT // PQ. Докажите, что точки A, P, X , Z лежат на одной окружности тогда и только тогда, когда A, Q, Y, T лежат на одной окружности

Дам подсказку к красивому решению) Оранжевые углы дают в сумме 180°.

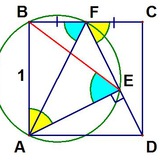
В квадрате AM=BN. Доказать, что из трех отрезков, на которые поделена диагональ, можно сложить треугольник с углом 60°.

по условию так сразу не скажешь, но предыдущую задачу можно решить при помощи выхода в пространство

попробуйте придумать геом. решение с такой подсказкой — или загляните в комментарии к прошлому посту

Моя с Вовой Конышевым задача с 1 дня майский сборов.

Дан вписанный четырехугольник ABCD. Докажите, что существует окружность, касающаяся следующих пяти окружностей: описанной окружности четырехугольника ABCD, вписанных окружностей треугольников ABC и ABD, C-вневписанной окружности треугольника ACD и
D-вневписанной окружности треугольника BCD.

выше обсуждалось ( https://tttttt.me/geometrykanal/1964 https://tttttt.me/geometrykanal/1965 ), что в описанном четырехугольники диагонали и отрезки, соединяющие точки касания, пересекаются в одной точке

докажите, что то же верно для криволинейных четырехугольников, составленных из двух коник (см. рис.)

можно считать это рекламой статьи В.Конышева «О дважды касающихся кониках и теореме Дезарга об инволюции» в новом Мат. просвещении (вып. 35), который дарили вчера на закрытии ММО

Выложили список приглашённых на финальный тур олимпиады Шарыгина 2025.