Можно ли сцепить концы у каждой из трех мишур так, чтобы получились три кольца, которые нельзя разцепить, но при разрезании любого из них они расцеплялись бы? А если мишур больше, чем три?

Вторая часть статьи про сопряжение Клауса Клоусона от Миши Сидоренко!

Если синие дуги имеют равную градусную меру, то красные отрезки имеют равную длину.

P.S. на предыдущей картинке была ошибка, спасибо обратившим внимание!

Неплохой гайд по инверсии.

коллега П.Пушкарь задал вопрос, а я не смог сходу ответить — предлагаю решить как задачу

Есть три точки на плоскости, треугольник. Тогда единственным образом определяются радиусы шаров таких, что они касаются плоскости в выбранных точках и друг друга. Внутрь этих шаров и плоскости можно вписать ещё шар. Где он коснется плоскости?

Это должна быть какая-то замечательная точка треугольника — какая?

коллега Д.Прокопенко напоминает такое прикольное утверждение:

Если сфера, вписанная в треугольную призму, касается нижнего основания в некоторой точке P, то верхнего основания она будет касаться в изогонально сопряженной с ней точке.

Кай находится в центре заколдованного круга с радиусом 100 метров. Каждую секунду он делает шаг длиной 1 метр. Перед каждым шагом он объявляет направление, в котором хочет шагнуть. Снежная королева имеет право заставить его сменить направление на противоположное (когда Кай находится внутри круга). Сможет ли Кай действовать так, чтобы выбраться из круга к Герде?

Со Старым Новым годом! 🎄

Теорема Карно Штейнера.
Даны два треугольника ABC и A_1B_1C_1. Оказалось, что перпендикуляры из точек A_1,B_1,C_1 на прямые BC, AC, AB пересекаются в точке P. Докажите, что перпендикуляры из точек A, B, С на стороны B_1C_1, A_1C_1, A_1B_1 пересекаются в одной точке.

1. Дана бесконечно удаленная прямая и на ней некоторая проективная инволюция. Докажите, что после поворота на 90 градусов она останется проективной инволюцией.
2. Докажите прошлую задачу используя 1.

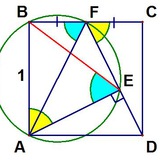
Дополнение к картинке К. Малевича.

Докажите, что если черный четырехугольник - квадрат, E и F - середины его сторон, то красный треугольник - правильный.

P.S. Хорошая учебная задача, которая следует из совпадения двух замечательных точек (центра описанной окружности и точки пересечения медиан) в красном треугольнике. А бывает ли так, что какие-то две замечательные точки совпадают, а треугольник - неправильный?

Давайте обсудим еще эту задачку)
1. Пусть дан шестиугольник ABCA_1B_1C_1 так, что никакие четыре точки не лежат на одной окружности, а прямые AA_1BB_1CC_1 пересекаются в одной точке. Что вы можете сказать про точки P такие, что окружности (APA_1), (BPB_1), (CPC_1) соосны.
2. Решите задачу используя 1.

Легко проверить, что если треугольник прямоугольный, то его полупериметр равен сумме диаметра описанной и радиуса вписанной окружностей. Попробуйте доказать геометрически обратное утверждение.

Разделить трапецию на рисунке а) на две подобных трапеции
б) на два подобных четырехугольника, не являющихся трапециями

Источник

Из четырех равных треугольников сложили выпуклый четырехугольник, у которого нет параллельных сторон. Какую форму могут иметь такие треугольники?

Задача Маркелова С.В. с Тургора

Дана коробка (прямоугольный параллелепипед), по поверхности (но не внутри) которой ползает муравей. Изначально муравей сидит в углу. Верно ли, что среди всех точек поверхности на наибольшем расстоянии от муравья находится противоположный угол? (Расстоянием между двумя точками считаем длину соединяющего их кратчайшего пути по поверхности параллелепипеда.)

P.S. Ответ в задаче неожиданный.

Не самая простая задача на построение

Даны две касающихся внешним образом окружности. Провести прямую так, чтобы она пересекла большую в точках A,B и коснулась меньшей в такой точке С, для которой CB=BA.

Все белые четырехугольники - квадраты. Тогда для каждого цвета сумма площадей полосатых многоугольников равна сумме площадей клетчатых.