задача выше входит в серию утверждений, про которую можно узнать из статьи Ф.Нилова в Квантике №11 за 2020 год:
https://old.kvantik.com/art/files/pdf/2020-11.13-15.pdf

подвижные чертежи к статье:
https://kvantik.com/extra/parall/

Пока самая красивая задача этого сезона. LMAO 2024 P3. Дан равносторонний оранжевый треугольник и точка P на его вписанной окружности. Точку P отразили относительно сторон оранжевого треугольника и получили красный треугольник. Далее отразили точку P относительно сторон красного треугольника и получили черный треугольник. Докажите, что описанная окружность черного треугольника касается вписанной и описанной оранжевого.

Еще одна задача со всеросса, в которой помогает гипербола. Окружности omega и omega' симметричны относительно точки A. Всероссийская олимпиада 2022 9.8.(А.Шевцов)

Забавный факт.

Продолжаем с этой конструкцией.

доказать, что большой четырехугольник описанный

задача, двойственная к предыдущей

(пусть будет и другая задача с визуально похожим условием, про которую в комментариях уже вспоминали)

доказать, что большой четырехугольник описанный

и чтобы завершить эту серию — утверждение, двойственное предыдущему, лемма о 6 окружностях

Просто задача.

KoMaL B. 5381

Кто-нибудь умеет просто доказывать такое утверждение: Дан треугольник ABC и точка P. Точки P_a,P_b,P_c симметричны относительно сторон ABC точке P. Точки O_a,O_b,O_c центры описанных окружностей треугольников PBC,PAC,PAB соответственно. Тогда, прямые AP_a,BP_b,CP_c пересекаются в одной точке тогда и только тогда, когда прямые AO_a,BO_b,CO_c пересекаются в одной точке

Статья на очень похожую задачу

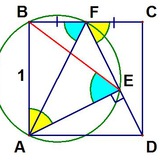
Зеленый четырехугольник — квадрат. Зеленый угол равен 45 градусов. Докажите, что разность красного и синего угла тоже 45 градусов.

Докажите, что точка пересечения высот треугольника, середины двух высот и основание третьей высоты лежат на одной окружности.

Может быть, кто-то в комментариях укажет первоисточник этой классической задачи

картинка на тему

«Что больше: 1⋅22+2⋅21+3⋅20+...+22⋅1 или 2²+4²+6²+...+22²?»

(из статьи А.Заславского в Квантике №6 за 2024 год)

Задача без картинки.
Дан треугольник ABC. Из точки A провели касательные к окружности с диаметром BC, которые касаются её в точках A_1,A_2. Аналогично определяются точки B_1,B_2,C_1,C_2. Докажите, что точки A_1,A_2,B_1,B_2,C_1,C_2 лежат на одной окружности.

Дан торт треугольной формы и коробка, которая имеет форму зеркально симметричного треугольника. Разрежьте торт на части и уложите их в коробку. Части можно поворачивать, но нельзя переворачивать

2024 RELMO 7. Можно ли восстановить(с помощью циркуля и линейки) разносторонний треугольник по точке Нагеля, точке Фейербаха и инцентру?

Дан прямоугольный треугольник ABC c углом A, равным 50 градусов. На катете BC взяли точки E и F так, что углы CAE и FAB равны по 10 градусов. Найти CE / FB