Очень крутая, но малоизвестная теорема (Теорема Витасса). Дан вписанный четырёхугольник ABCD. Его диагонали AC и BD пересекаются в точке P. Тогда, прямые Эйлера треугольников APB,BPC,CPD,APD пересекаются в одной точке. (Также можно задуматься, когда они являются параллельными)
Forwarded from Кроссворд Тьюринга (Vanya Yakovlev)
Популярная лекция по геометрии с недавнего Матпраздника
📄 Пока у нас пропуск, хочу поделиться записью лекции «Кривизна и углы» Александра Гайфуллина. Она посвящена свойствам кривых и поверхностей, за которыми стоит очень важное в геометрии понятие кривизны. В лекции много красивых доказательств (например, классно доказана теорема Эйлера), ну и вообще она отличная и по содержанию, и по доступности.
🎙 Александр Гайфуллин — победитель Матпраздника, а теперь член-корр. РАН, сотрудник МИАН, профессор МГУ.
Please open Telegram to view this post
VIEW IN TELEGRAM
YouTube
А.А.Гайфуллин. Кривизна и углы
Лекция на XXXV Математическом празднике (18.02.2024)
Forwarded from Математические этюды
Необычная для «Математических этюдов» премьера: «Теорема о двух кругах» https://etudes.ru/etudes/two-circles-theorem/ . Теорема даёт явное построение касательных к циклоидам – траекториям, описываемым фиксированной точкой окружности, катящейся без проскальзывания по некоторой гладкой линии.
Во-первых, необычная, так как просто объяснение геометрической теоремы. Но настолько красивой, что заслуживает своей отдельной экранизации. Кроме того, теорема дополняет цикл по понятию «огибающая» – сюжеты
«Парабола: изонить» https://etudes.ru/models/parabola-string-art/ ,
«Эллипс, гипербола, парабола: складывание листа бумаги» https://etudes.ru/models/conic-sections-paper-folding/ ,
«Кардиоида и нефроида» https://etudes.ru/models/cardioid-nephroid/ ,
«Каустики: нефроида и кардиоида» https://etudes.ru/etudes/caustic-nephroid-cardioid/ .
Теорема о двух круга, применённая к эпициклоидам, завершает доказательство того, что в цилиндрической чашке видна каустика в виде нефроиды, а в конической, когда лучи света параллельны образующей, – кардиоида.
Ну и во-вторых, премьера открывает новый жанр на Этюдах – повествование с анимированными рисунками.
Во-первых, необычная, так как просто объяснение геометрической теоремы. Но настолько красивой, что заслуживает своей отдельной экранизации. Кроме того, теорема дополняет цикл по понятию «огибающая» – сюжеты
«Парабола: изонить» https://etudes.ru/models/parabola-string-art/ ,
«Эллипс, гипербола, парабола: складывание листа бумаги» https://etudes.ru/models/conic-sections-paper-folding/ ,
«Кардиоида и нефроида» https://etudes.ru/models/cardioid-nephroid/ ,
«Каустики: нефроида и кардиоида» https://etudes.ru/etudes/caustic-nephroid-cardioid/ .
Теорема о двух круга, применённая к эпициклоидам, завершает доказательство того, что в цилиндрической чашке видна каустика в виде нефроиды, а в конической, когда лучи света параллельны образующей, – кардиоида.
Ну и во-вторых, премьера открывает новый жанр на Этюдах – повествование с анимированными рисунками.
etudes.ru
Теорема о двух кругах / Этюды // Математические этюды
Теорема о двух кругах: явное построение касательных к циклоидам, эпициклоидам и гипоциклоидам.
Forwarded from Kvantland | Квантландия | Интересные задачи и не только
Давно у нас не было геометрии. И сегодня новая 40-градусная задачка из серии "Геометрия для всех"!
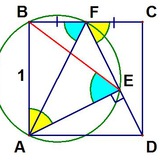
Вершины ломаной ABCD лежат на сторонах прямоугольника (см. рисунок). Все звенья ломаной равны, а два отмеченных на рисунке угла равны 40⁰. Чему равен угол CAD?
Вершины ломаной ABCD лежат на сторонах прямоугольника (см. рисунок). Все звенья ломаной равны, а два отмеченных на рисунке угла равны 40⁰. Чему равен угол CAD?
Геометрия-канал
На плоскости нарисовали несколько окружностей, после чего отметили все точки их пересечения или касания. Оказалось, что на каждой окружности лежит ровно n отмеченных точек и через каждую отмеченную точку проходит ровно n окружностей. Чему может быть равно…
Пример, когда n=4 (прямые - это окружности, проходящие через бесконечно удаленную точку)
Геометрия-канал
На плоскости нарисовали несколько окружностей, после чего отметили все точки их пересечения или касания. Оказалось, что на каждой окружности лежит ровно n отмеченных точек и через каждую отмеченную точку проходит ровно n окружностей. Чему может быть равно…
Пример, когда n=5 (прямые - это окружности, проходящие через бесконечно удаленную точку)
Forwarded from Олимпиадная геометрия
Добрая задача про равные окружности: красные окружности равны, докажите, что угол прямой
https://miro.com/app/board/uXjVKY1HfmI=/ & https://geometry.ru/dv.html — материалы по геометрии с сегодняшнего семинара учителей
Опять задача про Шалтая и Болтая. Закрашенный четырёхугольник является параллелограммом.
Геометрия-канал
https://miro.com/app/board/uXjVKY1HfmI=/ & https://geometry.ru/dv.html — материалы по геометрии с сегодняшнего семинара учителей
Даны две пересекающиеся окружности. Доказать, что длина отрезка BC не зависит от выбора точки A.
а кому это слишком просто — решите задачу Д.В.Прокопенко с устной олимпиады по геометрии 2010 года:
Серединные перпендикуляры к сторонам ВС и АС остроугольного треугольника АВС пересекают прямые АС и ВС в точках М и N. Пусть точка С движется по описанной окружности треугольника ABC, оставаясь в одной полуплоскости относительно АB (при этом точки A и B неподвижны). Докажите, что прямая MN касается фиксированной окружности.
можно считать, что всё это в качестве рекламы упомянутого семинара — вот, кстати, видеозапись: https://youtu.be/j-Z3-IfS8b4
а кому это слишком просто — решите задачу Д.В.Прокопенко с устной олимпиады по геометрии 2010 года:
Серединные перпендикуляры к сторонам ВС и АС остроугольного треугольника АВС пересекают прямые АС и ВС в точках М и N. Пусть точка С движется по описанной окружности треугольника ABC, оставаясь в одной полуплоскости относительно АB (при этом точки A и B неподвижны). Докажите, что прямая MN касается фиксированной окружности.
можно считать, что всё это в качестве рекламы упомянутого семинара — вот, кстати, видеозапись: https://youtu.be/j-Z3-IfS8b4
Forwarded from Олимпиадная геометрия
Media is too big
VIEW IN TELEGRAM
Касательную к вписанной окружности треугольника отразили относительно биссекстрис его внешних углов. Докажите, что три полученные прямые ограничивают треугольник, равный исходному.
Forwarded from MathOlymp
Разбираем 4 решения геометрической задачи с недавно прошедшей ММО!
YouTube
4 решения геометрии | 11.2, ММО 2024
Обсуждаем 4 решения геометрии 11.2 с Московской олимпиады 2024!
ВК: https://vk.com/math_olymp_vk
Телеграм: https://tttttt.me/matholymp_tg
По разным вопросам можете обращаться в комментариях или на почту ask.math.olymp@gmail.com
ВК: https://vk.com/math_olymp_vk
Телеграм: https://tttttt.me/matholymp_tg
По разным вопросам можете обращаться в комментариях или на почту ask.math.olymp@gmail.com
Дана пирамида, в которую можно вписать сферу. Точку касания этой сферы с основанием пирамиды спроектировали на рёбра основания. Докажите, что все проекции лежат на одной окружности.
Forwarded from Олимпиадная геометрия
Crazy fact
Два равных треугольника.
Любое количество окружностей.
Переставлять можно в любом порядке.
Два равных треугольника.
Любое количество окружностей.
Переставлять можно в любом порядке.
Forwarded from Олимпиадная геометрия
Добрая задача.
На сторонах треугольника построены равные прямоугольники. Докажите, что три прямых пересекаются в одной точке.
На сторонах треугольника построены равные прямоугольники. Докажите, что три прямых пересекаются в одной точке.
Вопрос без картинки.
Как построить(с помощью геогебры) треугольник такой,что его ортоцентр лежит на его вписанной окружности?
Как построить(с помощью геогебры) треугольник такой,что его ортоцентр лежит на его вписанной окружности?