Понедельничная разминка для старшеклассников! Парабола и треугольник

Угол в прямоугольном треугольнике.

Окружность, вписанная в прямоугольный треугольник, делит пополам отрезок между точкой ее касания с катетом и противоположной вершиной. Какой угол образует этот отрезок с катетом треугольника?

Это моя новая задача на прямоугольный треугольник. Ее может легко решить восьмиклассник, сложнее это будет сделать девятикласснику, а в одиннадцатом классе ее можно вообще не решить… А как она получится у вас?
Присылайте пока ответы, а не решения!

Три части
Любой равнобедренный треугольник можно разрезать на три части и сложить из них треугольник с прямым углом. Так же можно поступить с тупоугольным треугольником. Попробуйте это сделать!

А можно ли так разрезать остроугольный треугольник, я пока не знаю

Телеграм сделал возможность каналам публиковать истории.

Если у вас премиум-аккаунт и последняя версия, вы можете проголосовать за этот канал, чтобы включить  такую возможность. Хотя пока нет идей, как это лучше использовать.

Голосуют тут: https://tttttt.me/geometrykanal?boost

Давняя любимая задачка (с устной олимпиады 6-7 классов):

Придумайте шестиугольник, который нельзя разрезать диагональю на два четырехугольника.

Задача со вчерашнего творческого конкурса учителей:

В треугольнике ABC через точку F проведены чевианы AM, BL, CK, причем ∠CBL = ∠BAM, ∠BCK = ∠CAM. Окружности, описанные около треугольников BML и CMK, пересекают прямую AM в точках P и Q. Докажите, что A — середина отрезка PQ.

Треугольник на равные части

Каждый треугольник на верхних рисунках можно разрезать на 3 равные части. Можно доказать, что треугольники другой формы этим свойством не обладают.
На двух нижних рисунках показано, как разрезать любой треугольник на 4 равные части и как равносторонний - на 6 равных частей.
А можно ли какой-то треугольник разрезать на 5 равных частей?
Есть ли треугольник, который можно разрезать на 10 или даже 13 равных частей?

Пишите, на какое число равных частей вы можете разрезать треугольник и каким он должен для этого быть.

Сегодня стартовал Осенний марафон, который посвящен изучению планиметрии.

Каждый день в течение всего октября будут появляться маленький блок теории и несколько задач на её закрепление.
Это будет занимать 10-30 минут в день. И это бесплатно.

Первый день уже заканчивается, но доступ к нему продлен специально, чтобы все могли успеть присоединиться.

Регистрация на марафон через сайт
Регистрация через телеграм-бота

Всем привет! Понедельничная разминка №4!

В качестве первой задачи (для начинающих) я предлагаю задачу с регионального этапа олимпиады Эйлера 2021 года. Задача предлагалась во второй день под номером 7. Автор задачи С.Л. Берлов.

1. Точка M — середина стороны AC равностороннего треугольника ABC. Точки P и R на отрезках AM и BC соответственно выбраны так, что AP = BR. Найдите сумму углов ARM, PBM и BMR.

Вторая задача (для продолжающих) тоже про равносторонний треугольник и сумму углов. Первый пункт вполне доступен начинающим.

2. Сторона равностороннего треугольника поделена на n равных частей. Найдите сумму отмеченных на чертеже углов при (a) n=3; (b) при произвольном n.

Третья задача для сильных школьников. Предлагалась в 2006 году на финале ВсОШ в 11-ом классе под номером 4, но даже по мнению сайта problems.ru эта задача одна из самых простых в варианте. Автор задачи Л.А. Емельянов.

3. Биссектрисы BE и CF треугольника ABC пересекаются в точке I. Прямая EF пересекает описанную окружность в точках P и Q. Докажите, что радиус описанной окружности треугольника PIQ в два раза больше радиуса описанной окружности треугольника ABC.

Подарите ребенку востребованную IT-профессию! 

IT-специалисты получают высокие зарплаты, а ещё — поддержку от государства: ипотеку по выгодной ставке, отсрочку от армии и не только.

Если вы хотите помочь ребенку освоить фундаментальное IT-образование и получить дополнительные баллы к экзаменам.

Оставляйте заявку для школьников 3-10 классов и учитесь в Виртуальном классе Московской школы программистов.

Что ваш ребенок приобретет в будущем:

• Востребованную и надежную сферу работы.
• Возможность работать на зарубежные компании.
• Дополнительные баллы к ЕГЭ.

Московская школа программистов имеет государственную лицензию.

🎓 Выпускники школы:

• победители олимпиад: 90+ награды;
• чемпионы мира по робототехнике (WRO);
• чемпионы по кибербезопасности: золотая медаль на MOSCOW CTF SCHOOL;
• сдают ЕГЭ на 85-100 баллов;
• студенты МГУ, ВШЭ, МГТУ им. Баумана;
• сотрудники Яндекс, Сбер, Kaspersky, VK и других топовых IT-компаний.
#реклама

Жёлтый квадрат

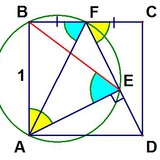
Если одна симметричная фигура вписана в другую, оси их симметрий могут совпадать. Однако так бывает не всегда: на рисунке вы можете видеть квадрат, косо вписанный в другую симметричную фигуру, образованную кругом и равнобедренным треугольником. Площадь такого квадрата чуть больше 48, и она — рациональное число.
Каким оно может быть?

Подписчик обнаружил интересный факт в геогебре, решения не знает... Мне тоже факт показался интересным.

Три эллипса с фокусами в вершинах треугольника проходят через центр вписанной окружности. Тогда три прямых, соединяющих вторые точки пересечения с соответствующими фокусами пересекаются в одной точке.

В прямоугольном треугольнике провели трисектрисы острых углов. Доказать, что зелёный треугольник правильный.

// почти Морли с закончившегося недавно Южного турнира