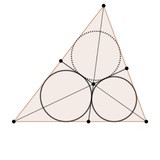
Задача 9.8, 10.8 просто удивительная!
🤡111🔥31🤮10🖕10👍3❤🔥2❤2✍1👎1😁1💯1
В треугольнике ABC проведены две изогонали AD и AE (т.е. зеленые углы равны). Красные точки — центры описанных окружностей треугольников ABD, ABE, ACD и ACE. Синие точки — центры их окружностей девяти точек. Докажите, что красный и синий четырехугольники вписаны, подобны и коэффициент подобия равен 2.
5🤯72❤8👍5🤮4👎2
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Добрая задача.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.
👍33❤7✍5👎3
Forwarded from Геометрия-канал (Grigory Merzon)
в Квант №3 вошла статья «Угол между радиусом и стороной» Ю.Блинкова и Д.Швецова
🔥42❤8🤔5👎3✍2👍1
Классика, которая служит отправной точкой множеству сюжетов и идей в олимпиадной геометрии 👆
🔥42👎3
Forwarded from NeuroGeometry (Savva Chuev)
Задача 62:
Четырехугольник ABCD вписан в окружность с центром O. Лучи BA и CD пересекаются в точке E, а лучи AD и BC в точке F. Оказалось, что ED = FD. Докажите, что инцентры треугольников ADE и CDF равноудалены от O
Четырехугольник ABCD вписан в окружность с центром O. Лучи BA и CD пересекаются в точке E, а лучи AD и BC в точке F. Оказалось, что ED = FD. Докажите, что инцентры треугольников ADE и CDF равноудалены от O
❤39👍3👎3✍2
Решение в комментариях образовалось, но напишу еще один интересный факт про эту конструкцию. Оказывается, радиусы вневписанной окружности и описанной окружности равны. Это более или менее задача Заславского с Московской олимпиады
✍23❤6👍4👎3
У WildMathing появился свой телеграм канал. Наверняка там будет прикольно!
👍26👎3❤1✍1
Forwarded from Wild Mathing
Manim — замечательная библиотека для математических анимаций. С ее помощью создаю все свои видео. Если будет интересно, могу делиться наработками. Снизу — код, сверху — результат
— О библиотеке
— 200+ примеров кода
— Курс для новичков
— Курс для продвинутых
#manim
from manim import *
import itertools as it
class Pyramid(ThreeDScene):
def construct(self):
a = 0.7 # длина стороны кубика
n = 5 # высота пирамиды (в кубиках)
pyramid = VGroup()
for k, j, i in it.product(range(n), repeat=3):
if (k + i < n) and (k + j < n):
cube = Cube(a).set_fill(BLUE_D, opacity=1)
cube.shift(a * np.array([i, -j, k]))
pyramid.add(cube.set_stroke(WHITE, 1))
self.set_camera_orientation(phi=PI/3, theta=-PI/3, focal_distance=500)
self.play(Write(pyramid))
self.wait()
— О библиотеке
— 200+ примеров кода
— Курс для новичков
— Курс для продвинутых
#manim
❤17👍4👎3✍2
Forwarded from Олимпиадная геометрия
Всем привет! А вот смотрите какое красивое утверждение! Автором задачи является Виктор Тебо (Victor Thebault). Эта задача предлагалась читателям в журнале American Mathematical Monthly в 1952 году.
Требуется установить, что периметры треугольников PQR и KLM равны!
Требуется установить, что периметры треугольников PQR и KLM равны!
🤔41❤13👎4🔥4✍2
Forwarded from Geometry Weekly
Из точек касания вневписанных окружностей со сторонами провели касательные к другим вневписанным окружностям. Тогда существует окружность, вписанная в получившийся шестиугольник
👍28🤔16🔥15✍6👎3❤1