По мотивам Румынской региональной (?) олимпиады
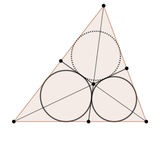
На картинке зеленые треугольники правильные. Вершины красного треугольника и синего треугольника — точки пересечения их сторон. Отмеченные точки это точки пересечения медиан треугольников. Доказать, что черные углы по 60 градусов
На самом деле можно добавить еще один треугольник, вершины которого точки пересечения сторон зеленых треугольников. Просто картинка будет чуть более загроможденной.
На картинке зеленые треугольники правильные. Вершины красного треугольника и синего треугольника — точки пересечения их сторон. Отмеченные точки это точки пересечения медиан треугольников. Доказать, что черные углы по 60 градусов
На самом деле можно добавить еще один треугольник, вершины которого точки пересечения сторон зеленых треугольников. Просто картинка будет чуть более загроможденной.
🤮30❤17😭7🗿6✍4👍4❤🔥2🤯1🤗1💘1
Агенты сообщили, что заочный тур олимпиады Шарыгина закончился!
Ближайший свободный длинный слот у меня будет в среду. Предлагаю в среду и провести стрим с прорешиванием задач с 17:00 до 21:00 по московскому времени!
Ссылки, явки и пароли появятся чуть позже! Надеюсь, будет задорно!
Ближайший свободный длинный слот у меня будет в среду. Предлагаю в среду и провести стрим с прорешиванием задач с 17:00 до 21:00 по московскому времени!
Ссылки, явки и пароли появятся чуть позже! Надеюсь, будет задорно!
❤74👍20🔥16❤🔥3🤯1
Уже сегодня с 17:00 до 21:00 по московскому времени!
https://www.youtube.com/live/pbmDAjQny7Q?si=SMY4KGCz26xxyyoU
https://www.youtube.com/live/pbmDAjQny7Q?si=SMY4KGCz26xxyyoU
YouTube
#10str. Прорешиваем заочный тур олимпиады Шарыгина 2025
В этом стриме мы будем прорешивать задачи заочного тура олимпиады Шарыгина, который завершился на днях. Я буду делать это без предварительной подготовки в режиме онлайн.
❤🔥41👍14🔥11❤1🤡1
Всем спасибо, кто пришел! Задача 17 объявляется не решившейся, пишите свои решения в комментариях! А еще пишите, какие задачи считаете красивыми или сложными с заочного тура!
❤45👍9❤🔥6😨3
Forwarded from Математические кружки | «МТ кружки»
Появились проходные баллы на заключительный этап ВсОШ по математике
1❤🔥56🤡28🔥12😢8💩6🍓5👍2🤮2❤1💘1
Forwarded from Дневник Бродского
Шедевр Алексея Доледенка с только что прошедшей ММО. На мой взгляд, пока что это лучшая задача сезона и лучшая геометрия ММО со времен звезды Кушнира.
Серые отрезки высоты, зеленые — биссектрисы понятно чего. Найдите сумму красных углов.
Серые отрезки высоты, зеленые — биссектрисы понятно чего. Найдите сумму красных углов.
💊104🤡46🔥20❤9🤮9🥰7👍3🤨3🖕2❤🔥1😢1
На сайте олимпиады Шарыгина появились официальные решения заочного тура!
В 11-ой задаче решения явно более простое, чем у меня 🤣
Да и в 10-ой... хотя про 10-ую я даже не уверен, что у меня правильное решение...
В 20-й тоже более изящное наблюдение, конечно)
https://geometry.ru/olimp/2025/2025_zaoch_sol_rus.pdf
В 11-ой задаче решения явно более простое, чем у меня 🤣
Да и в 10-ой... хотя про 10-ую я даже не уверен, что у меня правильное решение...
В 20-й тоже более изящное наблюдение, конечно)
https://geometry.ru/olimp/2025/2025_zaoch_sol_rus.pdf
🔥17❤3👍1👎1🖕1
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Теорема Дезарга = Теорема Паскаля.
Хотим например доказать теорему Дезарга для выделенных цветных треугольников. Тогда по обратной теореме Паскаля получаем, что красные точки на одной конике. Применяя теорему Паскаля для них, но в другом порядке получаем нужную коллинеарность.
Хотим например доказать теорему Дезарга для выделенных цветных треугольников. Тогда по обратной теореме Паскаля получаем, что красные точки на одной конике. Применяя теорему Паскаля для них, но в другом порядке получаем нужную коллинеарность.
👍68❤8🍌5✍3❤🔥2🤔2👎1🖕1
Мне нравится такая задача.
Педальные треугольники точек P и Q подобны естественным образом. Докажите, что прямая PQ проходит через центр описанной окружности треугольника!
// к дню рождения А.А.Заславского
Педальные треугольники точек P и Q подобны естественным образом. Докажите, что прямая PQ проходит через центр описанной окружности треугольника!
// к дню рождения А.А.Заславского
🎉44🔥8❤6👍2👎1🖕1
Forwarded from Непрерывное математическое образование
https://turgor.ru/problems/46/vs-46-baz-avt.pdf
https://turgor.ru/problems/46/vs-46-sl-avt.pdf
опубликованы задачи весеннего Турнира городов
https://turgor.ru/problems/46/vs-46-sl-avt.pdf
опубликованы задачи весеннего Турнира городов
❤9👎1
Forwarded from Геометрия-канал (Grigory Merzon)
в новый Квант (№2 за 2025 год) вошла статья Ф.Бахарева и Г.Челнокова про Why-точки, полуописанные окружности и прямую Эйлера
https://biblio.mccme.ru/node/281875
ранее на эту тему: https://tttttt.me/olympgeom/1265
https://biblio.mccme.ru/node/281875
ранее на эту тему: https://tttttt.me/olympgeom/1265
❤🔥43👍8❤6🍾6🔥4👎1