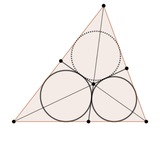
Для 11-классников, которые почему-то все еще готовятся к региону, хорошее упражнение по стереометрии.
В сечении правильного 2n-гранного угла плоскостью лежит 2n-угольник (не обязательно правильный). Ребра полученной пирамиды, соединяющие вершину с основанием, покрасили в шахматном порядке в красный и синий цвета. Докажите, что среднее гармоническое длин красных отрезков равно среднему гармоническому длин синих.
В сечении правильного 2n-гранного угла плоскостью лежит 2n-угольник (не обязательно правильный). Ребра полученной пирамиды, соединяющие вершину с основанием, покрасили в шахматном порядке в красный и синий цвета. Докажите, что среднее гармоническое длин красных отрезков равно среднему гармоническому длин синих.
😁51🤔15🔥9💊3❤🔥1👍1🌚1🍌1💋1
Прикольная задача 11.5 с сегодняшнего региона. Найдите сумму красного с синего угла. От себя, правда, скажу, что я против накладывания противоестественных лишних условий...
В треугольнике ABC с углом 100° при вершине A медианы BK и CN пересекаются в точке M. Прямая, проходящая через точку M и параллельная BC, пересекает описанную окружность треугольника AKN в точках Q и P. Найдите сумму углов BPC и BQC.
В треугольнике ABC с углом 100° при вершине A медианы BK и CN пересекаются в точке M. Прямая, проходящая через точку M и параллельная BC, пересекает описанную окружность треугольника AKN в точках Q и P. Найдите сумму углов BPC и BQC.
👎78👍16🤡11🤮5❤4🔥2😭2🍌1💋1
Forwarded from Математические кружки | «МТ кружки»
Условия задач 1-го дня региональной олимпиады ВсОШ и олимпиады Эйлера
👍36👎9✍6❤2💩1🍌1💋1💘1
Forwarded from Математические кружки | «МТ кружки»
Условия задач 2-го дня региональной олимпиады ВсОШ и олимпиады Эйлера
💩96👍9👎7🤮7🔥6❤5🎅5👏1🍌1💋1
Forwarded from Geometry Ukraine (Matthew Kurskyi)
Дано чотирикутник ABCD, в який вписано коло з центром I. Дотичні в точках А та С до описаного кола трикутника AIC перетинаються в точці Х, а дотичні в точках B та D до описаного кола трикутника BID перетинаються в точці Y.
Доведіть, що точки I, X та Y лежать на одній прямій.
Доведіть, що точки I, X та Y лежать на одній прямій.
👍44🤡28❤6👎3👏2🤓2🍌1💋1
Задача с израильского TST.
Хорошо известно, что биссектрисы внутренних углов вписанного четырехугольника ограничивают вписанный четырехугольник. Биссектрисы внешних углов — тоже ограничивают вписанный четырехугольник. Докажите, что центр описанной окружности исходного четырехугольника является серединой отрезка, соединяющего центры описанных окружностей четырехугольников, ограниченных биссектрисами.
Кстати, для треугольника вам такое утверждение, наверное, хорошо известно)
Хорошо известно, что биссектрисы внутренних углов вписанного четырехугольника ограничивают вписанный четырехугольник. Биссектрисы внешних углов — тоже ограничивают вписанный четырехугольник. Докажите, что центр описанной окружности исходного четырехугольника является серединой отрезка, соединяющего центры описанных окружностей четырехугольников, ограниченных биссектрисами.
Кстати, для треугольника вам такое утверждение, наверное, хорошо известно)
🔥51👍7🤩6❤2🤮2🤡2💩1🍌1💋1
Когда-то уже постил эту задачу, но она мне очень нравится, и она подходит тем, кто только начинает свой путь в геометрии, так что не жаль и повторить...
Зеленый четырехугольник — параллелограмм, нижняя вершина — середина стороны треугольника. Доказать, что верхняя лежит на биссектрисе.
Зеленый четырехугольник — параллелограмм, нижняя вершина — середина стороны треугольника. Доказать, что верхняя лежит на биссектрисе.
🔥55❤15💔4👍2💩1🍌1💋1🦄1
This media is not supported in your browser
VIEW IN TELEGRAM
❤33🥰7🔥5👍2🤮1🐳1🍌1💋1💘1