Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
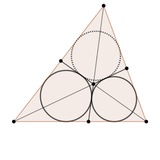
USEMO 2024 P3. Автор: Matsvei Zorka.
Докажите равенство зеленых.
Докажите равенство зеленых.
1🔥43👍4😈2🖕1
Так-так-так... Разыскиваются сильные команды, способные решить все задачи на JetBrains Math Challenge! Мне кажется, что в этот раз это будет не так просто... До окончания регистрации осталась всего неделя! А до самой олимпиады всего две недели (чуть меньше)!
(Кстати, это хороший способ потренироваться перед Колмом...)
(Кстати, это хороший способ потренироваться перед Колмом...)
JetBrains: Developer Tools for Professionals and Teams
JetBrains Academy Youth Challenge
Ultimate coding and math challenge for the school students from JetBrains Academy
🥰14❤6👏4👎2😁2❤🔥1👍1🖕1💊1
Forwarded from Задача дня (Юсуф Нагуманов)
Разминка №17(окружности Лукаса). Синие четырёхугольники - квадраты:
🥴47❤8🔥5🤯2👍1🥰1
Forwarded from Geometry Ukraine (Mykhailo Sydorenko)
Clawson_Conjugates_by Sydorenko Mykhailo.pdf
939.4 KB
Стаття про сопряження Клоусона.
Enjoy!
Enjoy!
👍41❤22🤡12🔥6🎄4❤🔥1⚡1🗿1
Шедевр от Кирилла Бельского из старшей лиги прошедшей сегодня устной командной олимпиады JetBrains. Задача, в которой есть секрет, которого, возможно, никто из участников и не увидел...
Серединный перпендикуляр к биссектрисе AL треугольника ABC пересекает стороны AB и AC в точках F и E, а описанную окружность Omega треугольника в точках P и Q. Касательные в точках P и Q к Omega пересекаются в точке R. Докажите, что описанные окружности треугольников AEF и PQR касаются.
Серединный перпендикуляр к биссектрисе AL треугольника ABC пересекает стороны AB и AC в точках F и E, а описанную окружность Omega треугольника в точках P и Q. Касательные в точках P и Q к Omega пересекаются в точке R. Докажите, что описанные окружности треугольников AEF и PQR касаются.
🔥37👍6❤5🤡4👎3💩3
Еще один шедевр от Георгия Галяпина и Станислава Кузнецова
Дан четырехугольник ABCD и точка P, не лежащая на описанных окружностях треугольников ABC, BCD, CDA и DAB. Пусть точки Pa, Pb, Pc и Pd} — изогонально сопряжены точке P относительно треугольников BCD, ACD, ABD и ABC соответственно. Оказалось, что прямые PaPc, AC и BD пересекаются в одной точке. Докажите, что через эту же точку проходит прямая PbPd.
Участники мне рассказали очень красивое решение, которое только добавляет этой задаче красоты (в дополнение к красивому решению, которое я и так знал).
Дан четырехугольник ABCD и точка P, не лежащая на описанных окружностях треугольников ABC, BCD, CDA и DAB. Пусть точки Pa, Pb, Pc и Pd} — изогонально сопряжены точке P относительно треугольников BCD, ACD, ABD и ABC соответственно. Оказалось, что прямые PaPc, AC и BD пересекаются в одной точке. Докажите, что через эту же точку проходит прямая PbPd.
Участники мне рассказали очень красивое решение, которое только добавляет этой задаче красоты (в дополнение к красивому решению, которое я и так знал).
1❤27🔥7❤🔥5🖕4🤮3💩3👍2
Еще одна задача из юниорской лиги. Мне нравится! Автор Алексей Доледенок.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы AB в точке D. Центр окружности — точка I. На луче DI выбрана точка E так, что ∠AEB = 45°.
Точки P и Q — основания перпендикуляров из E на стороны AC и BC соответственно. Описанная окружность треугольника DPQ пересекает стороны AC и BC в точках X и Y. Докажите, что AX = BY.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы AB в точке D. Центр окружности — точка I. На луче DI выбрана точка E так, что ∠AEB = 45°.
Точки P и Q — основания перпендикуляров из E на стороны AC и BC соответственно. Описанная окружность треугольника DPQ пересекает стороны AC и BC в точках X и Y. Докажите, что AX = BY.
🔥17❤6👍3👏1
Пост благодарности! Я бы хотел поблагодарить всех участников олимпиады за то, что они не поленились потратить свое воскресное время на решение задач, борьбу с лингвистическими и, порой, техническими трудностями, и это при том, что олимпиада эта не дает практически никаких бенефитов — без вас эта олимпиада была бы неполноценной.
Я бы хотел поблагодарить членов жюри, которые присоединились слушать задачи. Тоже ведь трудно заставить себя поучастовать в воскресном мероприятии, которое ничего кроме радости общения с единомышленниками тебе не принесет. Членам жюри тоже пришлось решать лингвистические и технические задачи, которые ставили перед ними участники. Спасибо вам! Хотелось бы, чтобы нас становилось больше и прослушка проходила в более спокойном режиме!
Я бы очень хотел поблагодарить авторов задач, которые не пожалели потратить свои творения на в общем-то никому пока неизвестную олимпиаду. В этом году, на мой взгляд, вариант получился значительно более интересным именно благодаря вам. Спасибо и тем, кто прислал свои задачи, но задачи нам почему-то не подошли. Я очень надеюсь, что вы не перестанете придумывать задачи и будете столь же отзывчивы на наши просьбы о помощи!
Я бы, конечно, хотел поблагодарить организаторов, потому что без их инициативы это мероприятие уж точно не состоялось бы. Организаторам всегда приходится не сладко, а работу их почти никто не видит.
Ну и конечно, я хотел бы поблагодарить своих коллег по методической комиссии!
Надеюсь олимпиада будет расти! И мы проведем ее еще лучше в следующем году. Пока что все задачи можно найти на аопсе. Но очень скоро мы доделаем и официальный файлик с условиями и решениями.
Я бы хотел поблагодарить членов жюри, которые присоединились слушать задачи. Тоже ведь трудно заставить себя поучастовать в воскресном мероприятии, которое ничего кроме радости общения с единомышленниками тебе не принесет. Членам жюри тоже пришлось решать лингвистические и технические задачи, которые ставили перед ними участники. Спасибо вам! Хотелось бы, чтобы нас становилось больше и прослушка проходила в более спокойном режиме!
Я бы очень хотел поблагодарить авторов задач, которые не пожалели потратить свои творения на в общем-то никому пока неизвестную олимпиаду. В этом году, на мой взгляд, вариант получился значительно более интересным именно благодаря вам. Спасибо и тем, кто прислал свои задачи, но задачи нам почему-то не подошли. Я очень надеюсь, что вы не перестанете придумывать задачи и будете столь же отзывчивы на наши просьбы о помощи!
Я бы, конечно, хотел поблагодарить организаторов, потому что без их инициативы это мероприятие уж точно не состоялось бы. Организаторам всегда приходится не сладко, а работу их почти никто не видит.
Ну и конечно, я хотел бы поблагодарить своих коллег по методической комиссии!
Надеюсь олимпиада будет расти! И мы проведем ее еще лучше в следующем году. Пока что все задачи можно найти на аопсе. Но очень скоро мы доделаем и официальный файлик с условиями и решениями.
3❤49🔥13👍8❤🔥1
Forwarded from Геометрия-канал (Grigory Merzon)
в «Олимпиадной геометрии» напомнили отличное утверждение
в прямоугольном треугольнике отметили точки касания (вне)вписанных окружностей со сторонами
доказать, что они лежат на двух окружностях
в прямоугольном треугольнике отметили точки касания (вне)вписанных окружностей со сторонами
доказать, что они лежат на двух окружностях
🔥27❤7🥱2🐳1
Добрая задачка с Baltic Way 2024
Пусть △ABC — остроугольный треугольник с описанной окружностью ω. Высоты AD, BE и CF треугольника ABC пересекаются в точке H. Точка K выбрана на прямой EF так, что KH и BC параллельны. Докажите, что точка, симметричная H относительно прямой KD, лежит на ω.
Пусть △ABC — остроугольный треугольник с описанной окружностью ω. Высоты AD, BE и CF треугольника ABC пересекаются в точке H. Точка K выбрана на прямой EF так, что KH и BC параллельны. Докажите, что точка, симметричная H относительно прямой KD, лежит на ω.
❤28🥰5✍3👏3👍2👎2