Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Добрая задача.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.
👍33❤7✍5👎3
Forwarded from Геометрия-канал (Grigory Merzon)
в Квант №3 вошла статья «Угол между радиусом и стороной» Ю.Блинкова и Д.Швецова
🔥42❤8🤔5👎3✍2👍1
Классика, которая служит отправной точкой множеству сюжетов и идей в олимпиадной геометрии 👆
🔥42👎3
Forwarded from NeuroGeometry (Savva Chuev)
Задача 62:
Четырехугольник ABCD вписан в окружность с центром O. Лучи BA и CD пересекаются в точке E, а лучи AD и BC в точке F. Оказалось, что ED = FD. Докажите, что инцентры треугольников ADE и CDF равноудалены от O
Четырехугольник ABCD вписан в окружность с центром O. Лучи BA и CD пересекаются в точке E, а лучи AD и BC в точке F. Оказалось, что ED = FD. Докажите, что инцентры треугольников ADE и CDF равноудалены от O
❤39👍3👎3✍2
Решение в комментариях образовалось, но напишу еще один интересный факт про эту конструкцию. Оказывается, радиусы вневписанной окружности и описанной окружности равны. Это более или менее задача Заславского с Московской олимпиады
✍23❤6👍4👎3
У WildMathing появился свой телеграм канал. Наверняка там будет прикольно!
👍26👎3❤1✍1
Forwarded from Wild Mathing
Manim — замечательная библиотека для математических анимаций. С ее помощью создаю все свои видео. Если будет интересно, могу делиться наработками. Снизу — код, сверху — результат
— О библиотеке
— 200+ примеров кода
— Курс для новичков
— Курс для продвинутых
#manim
from manim import *
import itertools as it
class Pyramid(ThreeDScene):
def construct(self):
a = 0.7 # длина стороны кубика
n = 5 # высота пирамиды (в кубиках)
pyramid = VGroup()
for k, j, i in it.product(range(n), repeat=3):
if (k + i < n) and (k + j < n):
cube = Cube(a).set_fill(BLUE_D, opacity=1)
cube.shift(a * np.array([i, -j, k]))
pyramid.add(cube.set_stroke(WHITE, 1))
self.set_camera_orientation(phi=PI/3, theta=-PI/3, focal_distance=500)
self.play(Write(pyramid))
self.wait()
— О библиотеке
— 200+ примеров кода
— Курс для новичков
— Курс для продвинутых
#manim
❤17👍4👎3✍2
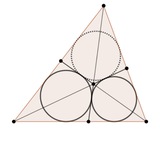
Forwarded from Олимпиадная геометрия
Всем привет! А вот смотрите какое красивое утверждение! Автором задачи является Виктор Тебо (Victor Thebault). Эта задача предлагалась читателям в журнале American Mathematical Monthly в 1952 году.
Требуется установить, что периметры треугольников PQR и KLM равны!
Требуется установить, что периметры треугольников PQR и KLM равны!
🤔41❤13👎4🔥4✍2
Forwarded from Geometry Weekly
Из точек касания вневписанных окружностей со сторонами провели касательные к другим вневписанным окружностям. Тогда существует окружность, вписанная в получившийся шестиугольник
👍28🤔16🔥15✍6👎3❤1
Forwarded from Олимпиадная математика ВсОШ | Дабромат
🐾 🐶 Стипендия от Таксы Дуси
Такса Дуся и команда преподавателей Дабромат хотят сделать качественное образование доступным как можно большему числу школьников по всей России. Поэтому по традиции мы готовы взять учеников на стипендию от Таксы Дуси, которая покроет полную стоимость обучения на летних курсах по геометрии.
Для кого❓
— Стипендия предназначена для ребят НЕ из Москвы, не имеющих финансовой возможности заниматься на наших курсах, но сильно желающих.
— Мы ожидаем, что стипендиаты будут учиться хорошо. За плохую успеваемость следует отчисление с курсов.
Что нужно сделать для получения стипендии❓
Необходимо прислать на @dabromat_support следующую информацию:
— Мотивационное письмо
— Рекомендация от преподавателя
— Перечень самых значимых олимпиадных успехов за последние два учебных года
Дедлайн подачи заявления: 20 мая включительно.
Результаты отбора мы сообщим 25 мая.
Распространение приветствуется — пусть как можно больше школьников получат доступ к качественному системному обучению математике! 📨
Такса Дуся и команда преподавателей Дабромат хотят сделать качественное образование доступным как можно большему числу школьников по всей России. Поэтому по традиции мы готовы взять учеников на стипендию от Таксы Дуси, которая покроет полную стоимость обучения на летних курсах по геометрии.
Для кого❓
— Стипендия предназначена для ребят НЕ из Москвы, не имеющих финансовой возможности заниматься на наших курсах, но сильно желающих.
— Мы ожидаем, что стипендиаты будут учиться хорошо. За плохую успеваемость следует отчисление с курсов.
Что нужно сделать для получения стипендии❓
Необходимо прислать на @dabromat_support следующую информацию:
— Мотивационное письмо
— Рекомендация от преподавателя
— Перечень самых значимых олимпиадных успехов за последние два учебных года
Дедлайн подачи заявления: 20 мая включительно.
Результаты отбора мы сообщим 25 мая.
Распространение приветствуется — пусть как можно больше школьников получат доступ к качественному системному обучению математике! 📨
🔥25👎13👍7❤5🤔4
Forwarded from Геометрия-канал (Grigory Merzon)
В квадрате AM=BN. Доказать, что из трех отрезков, на которые поделена диагональ, можно сложить треугольник с углом 60°.
2✍42👎18🔥6👍5❤1