🤡54👍30🔥8❤🔥4☃1🕊1💋1💅1🆒1
Forwarded from Олимпиадная математика ВсОШ | Дабромат
📚 КАК ЛЕГКО И ЭФФЕКТИВНО ПОДГОТОВИТЬСЯ К РЕГИОНУ ВСОШ ПО МАТЕМАТИКЕ И ОЛИМПИАДЕ ЭЙЛЕРА?
В одном из постов мы обмолвились об интенсиве, посвященном подготовке к региональному этапу ВсОШ по математике и олимпиаде Эйлера. И пришло время официально анонсировать его! 🤫
📌 Для кого: для учеников 8-11 классов.
📌 Дата проведения: 13-20 января.
Интенсив направлен не только на тщательную систематизацию знаний, но и дает возможность опробовать нашу систему обучения ребятам, которые пока не занимаются на курсах Дабромата. Мы иначе взглянули на формат интенсива в олимпиадной подготовке и сделали его еще структурированнее и эффективнее!
Что вас ждет❓
🔴 Три-четыре пары в день разного уровня сложности для каждого класса
🔴 Устная отслушка каждый день
🔴 Самостоятельное решение задач
🔴 Отправка заданий через Таксу Дусю и фидбэк в течение 24 часов
🔴 Оценка задач и их оформления по критериям региона ВсОШ и Эйлера
🔴 Пробная олимпиада в конце интенсива с экспертной проверкой, максимально приближенная к уровню региона
📌 Цена: 10 000 ₽ для новых ребят
Бесплатно для всех учеников II триместра основного четырехлетнего цикла.
📍 Но это еще не все!
📍 Данный интенсив обладает удобной системой кешбэка, позволяющей вернуть 100% стоимости курса.
Как вернуть деньги❓
Будущим призерам региона, занимающимся на интенсиве, вернется 50% стоимости, а победителям — все 100%.
Команда Дабромат дает гарантированный результат благодаря системному обучению на базе лучших математических центров и вы можете опробовать его вместе с нами: совсем скоро мы анонсируем старт продаж, расскажем про расписание и преподавателей.
Не пропустите! Будет действительно круто 🔥
В одном из постов мы обмолвились об интенсиве, посвященном подготовке к региональному этапу ВсОШ по математике и олимпиаде Эйлера. И пришло время официально анонсировать его! 🤫
📌 Для кого: для учеников 8-11 классов.
📌 Дата проведения: 13-20 января.
Интенсив направлен не только на тщательную систематизацию знаний, но и дает возможность опробовать нашу систему обучения ребятам, которые пока не занимаются на курсах Дабромата. Мы иначе взглянули на формат интенсива в олимпиадной подготовке и сделали его еще структурированнее и эффективнее!
Что вас ждет
📌 Цена: 10 000 ₽ для новых ребят
Бесплатно для всех учеников II триместра основного четырехлетнего цикла.
Как вернуть деньги
Будущим призерам региона, занимающимся на интенсиве, вернется 50% стоимости, а победителям — все 100%.
Команда Дабромат дает гарантированный результат благодаря системному обучению на базе лучших математических центров и вы можете опробовать его вместе с нами: совсем скоро мы анонсируем старт продаж, расскажем про расписание и преподавателей.
Не пропустите! Будет действительно круто 🔥
Please open Telegram to view this post
VIEW IN TELEGRAM
🔥17👍7❤6😱5🖕5🗿3👎2🤡1💋1💅1
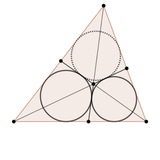
На тренировочные олимпиады МТ-кружков предложил вот такую задачу, которая попала в первую порцию. Не очень помню, откуда у меня в закромах такой факт.
Требуется доказать, что красные отрезки равны.
Кстати, разборы первой олимпиады уже опубликованы.
Требуется доказать, что красные отрезки равны.
Кстати, разборы первой олимпиады уже опубликованы.
🤪37👍11❤6💅2🆒2✍1🥰1😁1👀1💊1😎1
Во многим известной задаче 255 в одной точке пересекается много замечательных прямых, связанных с треугольником. А вот вам похожая задача.
В треугольнике ABC средняя линия, паралельная стороне AC, прямая, соединяющая основания высот из вершин A и B, симедиана из вершины A и прямая, проходящая через точку B параллельно касательной в вершине A к описанной окружности, пересекаются в одной точке.
В треугольнике ABC средняя линия, паралельная стороне AC, прямая, соединяющая основания высот из вершин A и B, симедиана из вершины A и прямая, проходящая через точку B параллельно касательной в вершине A к описанной окружности, пересекаются в одной точке.
❤47🔥9👍7⚡1💋1😨1
2020-02-11-where-is-orthocenter.pdf
183 KB
Решил завести рубрику "Разбор чужого листика".
Записал разбор листика Андрея Кушнира и Артемия Соколова про прямую Штейнера. Завтра постараюсь его выложить, а пока можете посмотреть сами задачи - по-моему хороший листик!
Записал разбор листика Андрея Кушнира и Артемия Соколова про прямую Штейнера. Завтра постараюсь его выложить, а пока можете посмотреть сами задачи - по-моему хороший листик!
👍26❤9🥰4💘3😁2💋1
Задача с тренировочной олимпиады МТ-кружков. Автор задачи Stanley Rabinowitz
Окружность ω с центром O касается внешним образом окружности Ω в точке T. Из точки A на окружности Ω проведены касательные AP и AQ к окружности ω. Прямые AT и PQ пересекаются в точке R. Докажите, что прямая RO пересекает окружность Ω в точке, диаметрально противоположной точке A.
Окружность ω с центром O касается внешним образом окружности Ω в точке T. Из точки A на окружности Ω проведены касательные AP и AQ к окружности ω. Прямые AT и PQ пересекаются в точке R. Докажите, что прямая RO пересекает окружность Ω в точке, диаметрально противоположной точке A.
❤14👍5🔥3💋1
This media is not supported in your browser
VIEW IN TELEGRAM
личный рекорд)
от стартового промпта до видео - полчаса. в основном на размеры видео, цвета, ну и как всегда пришлось повозиться с косяками в анимированной части. но это всегда было самое сложное...
стартовый промт в комментариях.
от стартового промпта до видео - полчаса. в основном на размеры видео, цвета, ну и как всегда пришлось повозиться с косяками в анимированной части. но это всегда было самое сложное...
стартовый промт в комментариях.
👍63❤🔥15🔥5❤2🍌2💋1