Друзья! Напоминаю, что сейчас и до конца марта идёт первый турнир нового сезона Квантландия с интерактивными задачами и головоломками. В этот раз мы сделали отдельно Турниры для 4-6 класса и для 7-9 класса, но участвовать могут и взрослые. Участие бесплатное, достаточно зарегистрироваться на сайте турнира https://math.kvantland.com/ и приступить к задачам (можно возвращаться к задачам в другой день и брать подсказки). Важно: лучше использовать ноутбук (не смартфон) и при регистрации на турнир на сайте использовать не gmail-почту, а альтернативную (yandex, mail,…), так как на gmail часто не приходит подтверждение регистрации. По итогам сезона мы наградим победителей!

Ну а сегодня задача по геометрии из предыдущего турнира для 7-9 класса:
На гипотенузе AB прямоугольного треугольника ABC отмечена точка D, из которой опущен перпендикуляр DE на катет BC. Найдите угол BCD, если AC = CD + DE, а угол CAE равен 23°.
Подписаться на Телеграм-канал
#Новости #ГеометрияДляВсех

Геометрия на клетчатой бумаге это здОрово! Автор олимпиадных задач, учитель математики школы “Летово” и создатель проекта “Беседы” Дмитрий Викторович Швецов провёл короткую интерактивную лекцию для детей и взрослых на Фестивале Квантика.

Youtube: https://youtu.be/2SRpIZ8qAS8
VK-video: https://vk.com/video-223907838_456239083

Одна из красивых задач с этой лекции была такой:
У вас есть клетчатый лист бумаги со стороной клетки 1 и линейка. Как построить квадрат площади 4/5?
Решения присылайте в комментариях, но не забывайте их скрывать!
#ГеометрияДляВсех #Видеоразборы

Придумал тут задачку, из которой хочется сделать аналог Сангаку:) Это такие деревянные таблички с чертежами к геометрическим теоремам. Они распространились в Японии во время изоляции страны в 17-19 веках. Эта задачка только что была на базовом Турнире Городов.

На стороне CD прямоугольника ABCD взята точка K. Из вершины B опустили перпендикуляр BH на отрезок AK. Оказалось, что отрезки AK и BH делят прямоугольник на три части, в каждую из которых можно вписать круг (см. рисунок). Докажите, что если два красных круга равны, то и зелёный круг им равен.

Условия всех задач можно найти здесь https://turgor.ru/problems/46/vs-46-baz-avt.pdf
А уже завтра сразу две отличные олимпиады: основной Турнир Городов и ММО. Желаю удачи участникам!
#ГеометрияДляВсех

Хорошая задача будит не только наш разум, но и наши эмоции.
В.В. Произволов

Мне снова встретилась отличная классическая задачка Вячеслава Викторовича Произволова. Хорошо подойдёт для эмблемы какой-нибудь математической олимпиады:)

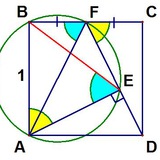
В квадрате построена четырёхзвенная ломаная так, что три угла равны 45 градусов, а одна из вершин совпадает с вершиной квадрата (см. рисунок). Докажите, что пять вершин этой ломаной лежат на одной окружности.

Изящный факт, не правда ли? Ставьте ❤️, если Вы со мной согласны.
#ГеометрияДляВсех