#задача

Задача, вернувшаяся с того света: Нарисовали треугольник ABC, отметили точки М1 — середину стороны ВС, L1 — основание биссектрисы из вершины А и ортоцентр Н. Потом всё, кроме этих трёх точек стёрли. Как восстановить треугольник по этим трём точкам?

Почему эта задача была похоронена, а потом возвращена к жизни (а заодно её решение) вы узнаете на семинаре учителей математики в среду в 19:00 по Москве.
https://mccme.ru/nir/seminar/

#задача
Источник: учебник геометрии 7 класса Максима Анатольевича Волчкевича для проекта «Математическая вертикаль»

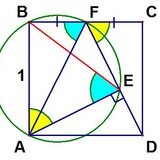
Площадь красного квадрата равна 1. Найдите площадь желтой плитки.

Источник: https://vk.com/problemaday
#задача

353. В треугольнике ABC ∠A = 45°; ∠C = 60°. На продолжении стороны BC за точку C взята точка D так, что BC = 2CD. Найдите ∠CAD.

#задача

Все фигуры - правильные многоугольники. Чему равна площадь фиолетового треугольника? #задача

#задача

Из сегодняшнего конкурса учителей:

Даны четыре концентрические окружности с радиусами 1, 2, 3 и 4. Существует ли квадрат,
вершины которого лежат по одной на каждой окружности?

Это задача методического блока с олимпиады учителей.

В заданиях этого блока могут содержаться математические ошибки (как в условиях «задач», так и в «ответах» и «решениях»). Если некорректно условие «задачи», требовалось объяснить, почему это так. Если неверно «решение» — указать все ошибки и недочёты, пояснить их суть, а затем привести верное решение.

#задача

https://www.geogebra.org/m/gmagufzq

задачка: треугольник равносторонний, доказать, что сумма красного и зеленого радиуса не зависит от положения прямой (via Ф.Нилов)

#задача

Взяли равнобедренный треугольник. Через вершину и середину основания провели произвольную окружность, пересекающую обе боковые стороны. Доказать, что сумма расстояний от двух точек пересечения до основания не зависит от выбора окружности.

(на самом деле, это задача-шутка в том смысле, что она здесь уже недавно была… но в другом виде — сможете узнать?)

#задача

К.Кноп сразу припомнил обобщение предыдущей задачи: для произвольного треугольника длина ломаной FCG не зависит от выбора окружности, проходящей через вершину C и основание биссектрисы D

(понятно ли, кстати, что предыдущая задача отсюда действительно следует?)

#задача

#задача доказать, что синий четырехугольник описанный

https://www.geogebra.org/m/utqyjjjq

#задача по мотивам разного недавнего (via А.Щетников):

доказать, что для сторон треугольника, углы которого относятся как 1:2:4, выполнено соотношение 1/a+1/b=1/c

(можно что-то посчитать, а можно найти и более геометрическое решение… видимо даже есть разные)

https://twitter.com/panlepan/status/1472218266420588548

эта #задача здесь уже была под номером 32 — а вот к ней красивые картинки

Правильный восемнадцатиугольник разбит на восемнадцать одинаковых пятиугольников. Докажите, что точки X, Y и Z лежат на одной прямой.

#задача

#Геометрия #Задача

Через точку внутри окружности Ω проведены три хорды, делящие ее на шесть криволинейных треугольников. В три из них, через один, вписали оранжевые окружности. Докажите, что сумма радиусов оранжевых окружностей не превосходит радиуса Ω.

Обсудить решение вы можете в нашем чате!

#геометрия #задача

Докажите, что пунктирная прямая проходит, через фиксированную точку.

#геометрия #задача

Прямая, проходящая через ортоцентр треугольника ABC пересекает его стороны AB и AC в точках D и E соответственно. Сторона BC, перпендикуляр к AB в точке D и перпендикуляр к AC в точке E образуют треугольник T. Докажите, что описанные окружности треугольников T и ABC касаются.