Forwarded from Олимпиадная геометрия
Много геометрических каналов, конечно, развелось... проще перечислить тех, у кого их нет... но я попробую в почти случайном порядке перечислить те, что есть.
Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...
У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...
Геометрия-канал старейший геометрический канал
Geometry Ukraine
Geometry Belarus
геометрия от Волчкевича
геометрия с Федором Ниловым
NeuroGeometry геометрия с не только лишь человеческим лицом
канал Ярослава Щербатова специалиста по Акопяну
канал Задача дня Юсуфа Нагуманова
Geometry Weekly автор скрывает свое имя... но мы то знаем...
У многих каналов есть свои чаты, но их уж я упоминать не буду. Наверняка, есть еще десяток, можете скинуть в комментариях, если действительно туда стоит заходить...
В четырехугольнике BCED три стороны равны (DB=BC=CE). Точка A внутри четырехугольника такова, что углы ABC и ACB равны \alpha и \beta, угол ABD равен 60°–(\alpha+2\beta)/3, а угол ACE равен 60°+(2\alpha+\beta)/3.
Докажите, что угол DAE равен \alpha+\beta
Источник: https://www.facebook.com/share/p/xn62fqozbsGxHcrt/?mibextid=oFDknk
Докажите, что угол DAE равен \alpha+\beta
Источник: https://www.facebook.com/share/p/xn62fqozbsGxHcrt/?mibextid=oFDknk
Forwarded from JustScience | Олимпиадная Математика (Вова)
#Геометрия #Задача
Через точку внутри окружности Ω проведены три хорды, делящие ее на шесть криволинейных треугольников. В три из них, через один, вписали оранжевые окружности. Докажите, что сумма радиусов оранжевых окружностей не превосходит радиуса Ω.
Обсудить решение вы можете в нашем чате!
Через точку внутри окружности Ω проведены три хорды, делящие ее на шесть криволинейных треугольников. В три из них, через один, вписали оранжевые окружности. Докажите, что сумма радиусов оранжевых окружностей не превосходит радиуса Ω.
Обсудить решение вы можете в нашем чате!
Геометрия-канал
Добрая задача. Докажите,что сумма площадей нечетных треугольников равна сумма площадей четных треугольников. (Одноцветные четырехугольники являются квадратами)
Интересно посмотреть, верно ли такое: если для четноугольника суммы площадей четных и нечетных треугольников равны для первого слоя, то аналогичное равенство сумм площадей четырехугольников будет верно и для всех слоев
Forwarded from Олимпиадная геометрия
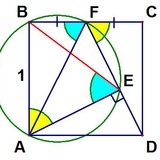
Из комментариев от пользователя Yu Ka. Красный и синий треугольники правильные. Доказать, что зеленый тоже правильный.
Forwarded from Геометрия с Ниловым
Симпатичная несложная "учебная" задача моего учителя М.А. Волчкевича. Попробуйте решить ее в уме.
В параллелограмме ABCD точка E – середина AD. Точка F – основание перпендикуляра, опущенного из B на прямую CE.
Докажите, что треугольник ABF – равнобедренный.
Рекомендую к прочтению его учебники Матвертикали 7-9, зеленый задачник Геометрия 7-8 и канал @volk_geometry
В параллелограмме ABCD точка E – середина AD. Точка F – основание перпендикуляра, опущенного из B на прямую CE.
Докажите, что треугольник ABF – равнобедренный.
Рекомендую к прочтению его учебники Матвертикали 7-9, зеленый задачник Геометрия 7-8 и канал @volk_geometry
Forwarded from AllМАT
Вот такая интересная задача мне попалась на днях: AD — биссектриса, J — точка на отрезке AD,
P — пересечение касательной к (АКL) в точке А и ВС. Докажите, что Р равноудалена от А и J.
Источник: устный тур «ТурГор» 2019, 6 задача.
Ждем ваши решения в комментариях!💪
Вот и весь AllМАТ🟣
P — пересечение касательной к (АКL) в точке А и ВС. Докажите, что Р равноудалена от А и J.
Источник: устный тур «ТурГор» 2019, 6 задача.
Ждем ваши решения в комментариях!
Вот и весь AllМАТ
Please open Telegram to view this post
VIEW IN TELEGRAM
Forwarded from Олимпиадная математика ВсОШ | Дабромат
⬜️ Финал олимпиады им. Шарыгина
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Федорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Федоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
Олимпиада имени И.Ф Шарыгина — это престижная геометрическая олимпиада для школьников 8–10 классов. Организатором выступает МЦНМО (Московский центр непрерывного математического образования).
Игорь Федорович Шарыгин — советский и российский математик и педагог, специалист по элементарной геометрии, популяризатор науки, автор учебников и пособий для школьников.
После окончания механико-математического факультета Московского государственного университета, Шарыгин остался в аспирантуре, а затем начал свою педагогическую карьеру в МГУ.
На протяжении многих лет Игорь Федорович посвятил себя не только преподаванию, но и популяризации математики. Он стал автором множества учебников и методических пособий, которые пользовались огромной популярностью и использовались в школах по всей стране.
В память об Игоре Федоровиче Шарыгине ряд российских научных организаций и учебных заведений решили ежегодно, начиная с 2005 года, проводить геометрическую олимпиаду.
Финальный тур 20-й олимпиады им. Шарыгина состоялся 30 июля - 2 августа. На решение задач участникам 8-10 классов отводилось два дня: 31 июля и 1 августа.
На сайте вы можете посмотреть с задания прошлых лет, а мы делимся с вами условиями этого года.
В комментариях можно найти решения👇🏻
Геометрия-канал
Photo
Отмечу крутую задачу от Григория Забазнова, а именно 9.8. Точки P и Q изогонально сопряжены в треугольнике ABC.
Forwarded from Григорий Забазнов
Isogonal_conjugate_points__To_prove_circle_through_4_points.pdf
361 KB
Forwarded from Григорий Забазнов
Более подробно решение, которое упомянул Петя Ким, можно прочитать в файлике выше
Please open Telegram to view this post
VIEW IN TELEGRAM