Задача подсказка. Дана парабола и точки A,B,C на ней так, что ее фокус является ортоцентром треугольника ABC. Тогда точка H лежит на вписанной окружности треугольника ABC.

Ладно, вот вам другая задача. А то говорят мало задач про многоугольники))

Даны два правильных шестиугольника.

(a) Докажите, что сумма площадей красных четырехугольников равна сумме площадей синих.

(b) Докажите, что сумма квадратов площадей красных четырехугольников равна сумме квадратов площадей синих.

Авторы: Fotis Dellaportas
и В.Н. Дубровский

Через общую точку двух окружностей проводят всевозможные прямые, которые вторично пересекают эти окружности в точках A и B. Доказать, что ГМТ середин AB — окружность.

Bulgaria NMO 2024, Problem 6

Вот такая симпатичная и несложная задача была в это воскресенье на устной олимпиаде по геометрии (Автор: Д. Прокопенко):

B треугольнике ABC провели биссектрису BL. Докажите, что центры окружностей, вписанных в треугольники ABL и CBL, а также центры вневписанных окружностей этих треугольников, касающихся стороны BL, лежат на одной окружности.

Красиво, не правда ли?

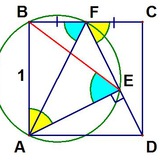
Добрая задача. Два подобных прямоугольных треугольника расположены как показано на рисунке. Докажите, что центр синей окружности попадает на катет.

(автор Д.В. Фомин)

на сайте устной олимпиады появились условия и решения проходившей в воскресенье геометрической олимпиады

https://olympiads.mccme.ru/ustn/usl24ge.pdf

https://olympiads.mccme.ru/ustn/resh24ge.pdf

Лекция Дмитрия Швецова про геометрические шедевры М.А.Волчкевича.

Ну ещё я придумал обобщение одной из задач,которые разбираются в этой лекции.

Материалы по теореме Понселе

https://www.mathnet.ru/links/8e3f7d9cd73539d209e1f366c982180c/mo426.pdf

https://www.mathnet.ru/links/b73f36f15d9e754735cb1db12778beb6/kvant1817.pdf

https://mathworld.wolfram.com/PonceletsPorism.html

https://www.geogebra.org/classic/mcfys5q6
https://www.geogebra.org/classic/bjpvtpwm
https://www.geogebra.org/classic/dx3sgmnb

На основании равнобедренного треугольника во внешнюю сторону построена дуга окружности. Две прямые, проходящие через вершину треугольника, делят на три равные части как основание, так и дугу. Найти отношение величины углы при вершине треугольника к градусной мере построенной дуги.

BC || DE. Докажите,что существует синяя окружность.

Найдите общее с прошлой задачей.

Про полувписанные окружности интересная лемма. Доказать, что общая касательная параллельна хорде.

Очень крутая задача с очень крутым решением. JBMO Shortlist 2022 G6. Proposed by Nikola Velov, Macedonia.

Этот листок даю в 8 классе на кружке, а основные факты (на картинках) на уроках. Сильные запоминают в 8 , слабые -- в 9, и то не все, конечно.

Продолжаю выкладывать задачки с полувписанными окружностями.