Books
Mathematics_is_the_Poetry_of_Science_Cédric_Villani_Z_Library.pdf
For those who don't know Villani or his works:
https://inv.nadeko.net/watch?v=ijQM0IpTKmY
https://inv.nadeko.net/watch?v=ijQM0IpTKmY
Hausdorff Center for Mathematics | Invidious
Panorama of Mathematics: Cédric Villani
Panorama of Mathematics
To celebrate the tenth year of successful progression of our cluster of excellence we organized the conference "Panorama of Mathematics" from October 21-23, 2015. It outlined new trends, results, and challenges in mathematical sciences.…
To celebrate the tenth year of successful progression of our cluster of excellence we organized the conference "Panorama of Mathematics" from October 21-23, 2015. It outlined new trends, results, and challenges in mathematical sciences.…
1844. Grassmann publishes the first full exposition of his system, his Die lineale Ausdehnungslehre, ein neuer Zweig der Mathematik dargestellt and durch Anwendungen auf die ubrigen Zweige der Mathematick, wie auch auf der Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert. Whereas on the title page of Hamilton’s Lectures on Quaternions, Hamilton was identified by a large array of titles and memberships, Grassmann’s title page identified him only as “Lehrer an der Friedrich Wilhelms Schule zu Stettin.” The book attracts almost no attention and about 600 copies of it were in 1864 used for waste paper.
Grassmann’s Die lineale Ausdehnungslehre (Linear Extension Theory) demonstrated deep mathematical insights. It also in one sense contained much of the modern system of vector analysis. This, however, was embedded within a far broader system, which included n-dimensional spaces and as many as sixteen different products of his base entities (including his inner and outer products, which are respectively somewhat close to the our modern dot and cross products). Moreover, Grassmann justifies his system by philosophical discussions that may have put off many of his readers. The abstractness of his presentation and the originality of his insights also contributed to the difficulties readers had in comprehending Grassmann’s message, as is evident from comments made by various mathematicians who had struggled with the book. Möbius, for example, labeled it unreadable, Baltzer reported that reading the book made him feel “dizzy and to see sky blue before my eyes,” and Hamilton wrote De Morgan that to read the Ausdehnungslehre he would have to learn to smoke.
1845. After Grassmann’s unsuccessful efforts to persuade Möbius to write a review of his book, Grassmann, at Möbius’s urging, writes a review of his own book—the only review his book received! He also publishes a paper containing a new discovery in electrical theory that he had derived using his new methods. The result: more neglect, until the 1870s when Clausius made the same electrical discovery and published it, only then realizing that Grassmann had preceded him.
Michael Crowe, A History of Vector Analysis (1969)
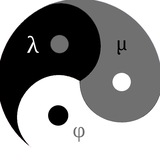
(φ (μ (λ)))
1844. Grassmann publishes the first full exposition of his system, his Die lineale Ausdehnungslehre, ein neuer Zweig der Mathematik dargestellt and durch Anwendungen auf die ubrigen Zweige der Mathematick, wie auch auf der Statik, Mechanik, die Lehre vom Magnetismus…
Apart from Abel (dying at age 24 out of dire poverty) and Galois (dying at 23 due to stupid politics), Grassmann suffered an unnecessarily cruel fate with regards to his mathematics. Goes on to say how a lack of being amongst the "chosen ones" can hamper your credibility.
Grassmann was prolific and too ahead of his time, he was able to foresee a vector space in its fullest manner, opening a whole new branch of mathematics. Without Grassmannians and exterior products you can do nothing in differential geometry.
No wonder that even though Grassmann didn't receive credit during a big part of his life, he receives only lip service today. Due to the lack of historical engagement among students and worse teachers of mathematics, nobody actually ever read a page of Grassmann's brilliant work, it's outrageous how they could put it to using as 'waste paper'.
He did not give up though, he went on to use his mathematics in physics, he studied linguistics for much of his later half, publishing one of the most comprehensive texts in Sanskrit and its relationship to Greek. His work on the Rig Veda is an often cited reference. Yet, no one today even in linguistics hears about Grassmann but only in passing, let alone compare his math and linguistics.
Just as Galois opened several branches of mathematics without living through any of them, Grassmann envisioned more things than what could be within the mathematical intuition of his time.
Grassmann was prolific and too ahead of his time, he was able to foresee a vector space in its fullest manner, opening a whole new branch of mathematics. Without Grassmannians and exterior products you can do nothing in differential geometry.
No wonder that even though Grassmann didn't receive credit during a big part of his life, he receives only lip service today. Due to the lack of historical engagement among students and worse teachers of mathematics, nobody actually ever read a page of Grassmann's brilliant work, it's outrageous how they could put it to using as 'waste paper'.
He did not give up though, he went on to use his mathematics in physics, he studied linguistics for much of his later half, publishing one of the most comprehensive texts in Sanskrit and its relationship to Greek. His work on the Rig Veda is an often cited reference. Yet, no one today even in linguistics hears about Grassmann but only in passing, let alone compare his math and linguistics.
Just as Galois opened several branches of mathematics without living through any of them, Grassmann envisioned more things than what could be within the mathematical intuition of his time.
🫡1
Forwarded from Programming Deadlock
11-ghuloum.pdf
581.7 KB
An Incremental Approach to Compiler Construction
Forwarded from ⸙anachronistic leaves🌿
Images created solely using mathematical equations by mathematical artist Hamid Naderi Yaganeh.
🤯10🤩3😍3❤2👍1🔥1